Annotated Bibliography 2020 11.17-11.20
虽然自己还有好几个没有更新完，但是为了组会和AWOC就先把这个做出来吧。。。
IOP-Reflectance relationships revisited Accepted
doi: 10.1029/2020JC016661.
Introduction
The quasi-single scattering approximation (QSSA) (Gordon 1973; Gordon et al., 1975) models are widely employed in standard ocean colour processing and applications because they provide an explicit relationship between IOPs and rrs(λ), as formulated by Gordon et al. (1988), coupled with a simple relationship for converting Rrs(λ) to rrs(λ) (Lee et al., 2002). The weakness of QSSA models is their inability to account for multiple scattering effects and their lower accuracy, compared to radiative transfer (RT) codes (Werdell et al., 2018).
On the other hand, forward RT models such as HydroLight (Sequoia Scientific, Inc.) can provide the full radiance distribution below and above the water, as a direct solution to the RT equation (Mobley, 1994). Therefore, given a set of input IOPs and appropriate boundary conditions, it is possible to generate precise estimates of a full set of AOPs, including rrs(0-, λ) and Rrs(0+, λ).
However, the inverse problem of determining IOPs from AOPs is not straightforward and relies on empirical and/or semi-analytical relationships.
Early work in this area focused on irradiance reflectance below the sea surface, R(0-,λ) (nondim), defined as the ratio of the upwards to downwards planar irradiances, Eu(0-,λ) (Wm-2nm-1)/ Ed(0-,λ) (Wm-2nm-1), as this was both practically measureable with available instrumentation and computationally convenient (e.g. Kirk, 1984).
At least two different expressions are found to approximate the relationship between R and absorption and backscattering coefficients
Morel and Prieur (1977), modelling the results from radiative transfer calculations, found that \[ R(0^{-},\lambda)=f\frac{b_{b}(\lambda)}{a(\lambda)}, \] while Gordon et al. (1975) showed that \[ R(0^{-},\lambda)=F(\frac{b_b(\lambda)}{a(\lambda)+b_b(\lambda)}) \] while f in Eq(1) is a variable in natural conditions(Morel & Gentili 1991; 1996) accounting for most of the directional effects due to changes in the light field, degrees of multiple scattering and in water bio-optical characteristics. F in Eq(2) represents a polynomial function with factors for up to 3rd order given in the original paper.
The exact form of F in Equation 2 (2nd or 3rd order polynomial) and the associated polynomial coefficients have not been unambiguously established for all situations, though in several cases a second order polynomial has been adopted (e.g. Feng et al., 2005).
Rrs(0+,\(\lambda\)) measurements are converted to below surface rrs(0-,\(\lambda\))using \[ R_{rs}(0^+,\lambda)=T.r_{rs}(0^-,\lambda) \] where T is a transmission factor incorporating information including the Fresnel transmittance from water to air, the refractive index of seawater (invoking the n2 law of radiances) and several additional factors to deal with propagation of downwards irradiance (see Mobley 1999 and IOCCG 2019 for more details). The resulting conversion factor T exhibits only limited variability (0.50 < T < 0.57) and is usually assumed to have a value of 0.54.
Morel and Prieur (1977) adapted equation (1) to express sub-surface remote sensing reflectance rrs(0-,λ) as a function of the ratio bb(λ)/a(λ) (wM from here onward): \[ r_{rs}(0^-,\lambda)=\frac{L_u(0^-,\lambda)}{E_d(0^-,\lambda)}=\frac{R(0^-,\lambda)}{Q}=\frac{f}{Q}\frac{b_b(\lambda)}{a(\lambda)}=\frac{f}{Q}w_M \] where Q (sr) is the bidirectional function defined by Morel and Gentili (1996) as the ratio of upwards irradiance Eu(0-,λ) to upwards radiance, Lu(0-,λ), and expresses the non-isotropic character of the radiance distribution1.
In contemporary ocean colour processing (Werdell et al., 2018), rrs(0-,λ) is more often expressed as a function of IOPs following the approach of Gordon et al. (1988) using the ratio of bb(λ)/[a(λ)+bb(λ)] (wG from here onward) \[ r_{rs}(0^-,\lambda)=\frac{L_u(0^-,\lambda)}{E_d(0^-,\lambda)}=\frac{R(0^-,\lambda)}{Q}=g_0w_G+g_1w_G^2 \] Taking Equations 3, 4 and 5 together, it is clear that Rrs(0+,λ) can be related to IOPs through either wG or wM. However, the apparently simple form of equations 4 and 5 is deceptive. f and Q are variables from a series of paper.
Morel and Gentili (1991, 1993, 1996) explored variability in f and Q, with the f/Q factor found to be variable in the range 0.075- 0.12 in oceanic (Case 1) waters and affected by solar zenith angle, sensor viewing geometry, in- water constituent concentrations and wavelength.
Furthermore, in coastal (Case 2) waters, additional concentrations of CDOM and mineral particles that do not co-vary with the chlorophyll concentration were expected to influence the variability of f/Q, though this variability was found to be minimal in the nadir viewing direction and the f/Q factor was almost insensitive to different wavelengths when the Sun is at the zenith (Loisel & Morel, 2001)
One possible reason for the relative popularity of IOP-reflectance relationships operating on wG is that the quadratic form expressed in Equation 5 captures some of the nonlinear behavior in the relationship with IOPs that is less obviously elucidated in the LUT approach for f/Q. The limiting factor for Gordon-style versions of the relationship with IOPs stems from failure to achieve consensus on a single form or set of coefficients that performs equally well across the known range of variability for natural waters.
Gordon et al. (1988) suggested a quadratic form with g0=0.0949 and g1=0.0794 for Case 1 waters, while for highly scattering coastal waters Lee et al. (1999) suggested g0=0.084 and g1=0.17. Later Lee et al. (2002), aiming at applying the forward model to both coastal and open-ocean waters, proposed average values of the coefficients from previous studies, g0=0.0895 and g1=0.1247.
Subsequently, focusing on above surface Rrs, Albert and Mobley (2003) and Park and Ruddick (2005) developed 4th order polynomial relationships in deep and shallow waters, while more recently Lee et al. (2011) and Hlaing et al. (2012) presented 2nd and 3rd order polynomial variants respectively.
Whilst there has been considerable improvement in our understanding of IOP-reflectance relationships since the pioneering studies by Morel and Gordon, there remains confusion in the field about the relative merits of wM and wG approaches. Moreover, there is an outstanding requirement to develop easily implemented relationships that permit end users to relate IOPs and reflectance values for both above and below surface reflectances corresponding to remote sensing and in situ applications. Most importantly, it is essential that the performance of any such relationship is equivalent across the wide range of concentrations of optical constituents found in natural waters and can be applied equally well in both clear Case 1 waters and optically complex Case 2 waters.
Aim of this study
Exploit the strength of forward RT modelling to generate a consistent set of IOPs and corresponding simulated rrs and Rrs values which enables investigation of IOP-reflectance relationships across a wide variety of optically complex water conditions.
Material and method
Field data
In situ Optical Measurements
All in situ data used in this study were collected in March 2009 during the BP09 cruise in the Ligurian Sea (Figure 1). Located in the northwest part of the Mediterranean Sea, this area includes both deep clear oceanic waters (considered Case 1) and shallow turbid coastal waters (considered Case 2). Among 60 sampled stations, 11 offshore stations and 23 onshore stations returned sufficient data set for the purpose of this work. A detailed description of the sampling location, data and methods can be found in McKee et al. (2014), Bengil et al. (2016) and Ramírez- Pérez et al. (2018)
Laboratory measurement
Bio-optical model developement
Following the methodology reported in Ramírez-Pérez et al. (2018) for Case 2 waters, each total IOP can be considered as the sum of partial IOPs, and each partial IOP can be expressed as the product of SIOPs, and associated constituent concentrations:
\[ a_{Tot}(\lambda)=a_{ph}^{*}(\lambda)CHL+a_{bdet}^{*}(\lambda)CHL+a_{ndet}^{*}(\lambda)MSS+a_{cdom}^{*}(\lambda)CDOM+a_w(\lambda) \]
\[ b_{Tot}(\lambda)=b_{ph}^{*}CHL+b_{ndet}^{*}(\lambda)MSS+b_w(\lambda) \]
\[ c_{Tot}(\lambda)=a_{Tot}(\lambda)+b_{Tot}(\lambda) \]
\[ b_{b \ Tot}=b_{bph}^{*}(\lambda)CHL+b_{bndet}^{*}(\lambda)MSS+b_{b \ w}{\lambda} \]
where the subscripts represent the following five bio-optical constituents: phytoplankton (ph), biogenic detritus (bdet), non-biogenic detritus (ndet), coloured dissolved organic material (cdom) and pure water (w). The constituent concentrations are: chlorophyll, CHL, absorption of coloured dissolved organic material at 440 nm, CDOM, and mineral suspended solids, MSS (the non- biogenic detrital component of total suspended solids). Here
Here the detrital particulate absorption has been considered as the sum of two separate biogenic and non-biogenic components. Unfortunately it is not possible to experimentally partition scattering and backscattering measurements so the level of discrimination possible for these parameters is reduced.
Biogenic partial IOPs are assumed to co-vary with CHL, while the non-biogenic partial IOPs are assumed to co-vary with MSS
In this study, only values at each standard AC-9 wavelength have been considered.
These SIOPs have been determined by simple linear regressions forced through zero of partitioned IOPs against associated constituent concentrations from surface water samples.
The optimal SIOP value has been estimated using the linear regression slope with the 95% Confidence Interval (CI) representing the associated uncertainty (Figure 2, red dashed lines).
Figure 2. Material-specific IOPs (black lines) with 95% confidence bounds (red dashed lines) obtained by linear regression at 9 wavelengths. (a) CHL-specific phytoplankton absorption – full data set. (b) CDOM absorption normalised at the signal at 440 nm – full data set. (c) CHL-specific biogenic detrital absorption – offshore data set. (d) CHL-specific phytoplankton scattering – offshore data set. (e) MSS-specific nonbiogenic detrital absorption coefficient – onshore data set. (f) MSS-specific nonbiogenic detrital scattering coefficient – onshore data set. SIOPs in (a)-(f) are recalculated SIOPs from Ramírez-Pérez et al. (2018) after further quality control measures were implemented. (g) the CHL-specific phytoplankton backscattering coefficient has been determined by linear regression forced through zero applied to the offshore data set, and (h) MSS-specific non biogenic detrital backscattering coefficient has been determined with the same methodology. Regressions on backscattering coefficients returned average R2 values of 0.78
In addition to the previously provided SIOPs for partitioned absorption and scattering coefficients, the material-specific backscattering coefficients are presented here following the same methodology. The chlorophyll-specific phytoplankton backscattering coefficient, shown in Figure 2g, was determined using data from offshore stations (considered Case 1 waters), where the particle population is assumed to be biogenic in origin. However,it is assumed to be representative of algal and biogenic detrital backscattering for all stations, offshore and onshore.
For onshore stations (considered Case 2 waters) it is assumed that there will be an additional non-biogenic contribution, \(b_{bndet}(\lambda)\), that can be found after subtraction of the water and biogenic contribution $(b_{bph}^{}()CHL) $ from \(b_{bTot}(\lambda)\). The MSS-∗ specific non biogenic detrital backscattering coefficient, \(b_{bpndet}^{*}(\lambda)\)shown in Figure 2h was obtained by regressing \(b_{bpndet}(\lambda)\) against MSS.
Radiative transfer simulations
Input IOPs for the simulations were generated by populating the bio-optical model, described in the previous section at 9 standard AC-9 wavelengths(412, 440, 488, 510, 532, 555, 650, 676, and 715 nm). A total of 1690 unique combinations of constituent concentrations and associated IOPs were calculated from log-spaced distributions of constituent concentrations in specific ranges (0.01<CHL<100 mg/m3, n = 13; 0.01<MSS<100 g/m3, n = 13; 0.01<CDOM<10 m- 1, n = 10)).
The data set of modeled IOPs was arranged in the form of 1690 virtual AC-9 and BB- 9 type files in the Matlab® environment (MathWorks Inc.).
The radiative transfer numerical model HydroLight 5.2 (Sequoia Scientific Inc.) was used to process the input IOP data and generate a synthetic dataset of remote sensing reflectance spectra, both below and above the sea-air interface, rrs(0-, λ) and Rrs(0+, λ) respectively.
Flow of this simulation: SIOP->IOP->AOP, the first step just randomly input, the second step is using Hydrolight, this process is reversion/forward
Based on the considered constituent concentration ranges, the total absorption at 412 nm, a(412), was in the range 0.0218–27.1346 m−1, while the total backscattering coefficient, bb(412),varied from 0.0036 to 2.3240 m−1, where the minimum (maximum) values represent the total IOPs when all the constituent concentrations are at their lowest (highest). Pure water absorption and scattering values were taken from Pope and Fry (1997) and Smith and Baker (1981).
Sky radiance was modelled using RADTRAN-X (Gregg & Carder, 1990) with no wind and the mean Earth-Sun distance was employed.
Other atmospheric conditions such as sea-level pressure, relative humidity, horizontal visibility, and ozone concentration were set at default values, which are described in the HydroLight 5 technical documentation (Mobley & Sundman, 2008).Raman (inelastic) scattering by water itself is ubiquitous and was considered since it is easy to model without any extra information, while fluorescence emissions due to chlorophyll and CDOM were not included, due to lack of information about fluorescence quantum yields.2
Result
Establishing the nature of IOP - reflectance relationships
f/Q and T
Variations in the bidirectional properties of the radiant flux leaving the water and returned toward the atmosphere have been extensively studied (Morel & Gentili, 1991, 1993, 1996; Morel et al., 2002). The term f/Q in Equation 4 implicitly describes the magnitude of these variations, mainly due to changes in the light field geometry and bio-optical characteristics of the water body. Figure 3 shows distributions of f/Q as obtained in this study from RT simulations, calculated from Equation 4.These results are broadly consistent with Morel and Gentili (1993) who found values in the range 0.075 – 0.12. f/Q also influenced by variations in sun angles and viewing geometries. This is confirmed in Figures 4c and 4d where it can be seen that changing solar zenith angle has a small but defined impact on relationships between Rrs and both wM and wG.
In the present study, unless otherwise stated, the results refer only to a zenith Sun and a vertical viewing direction, meaning that the variability of the f/Q factor here is due mainly to differences in water constituent concentrations
Figure 3. Frequency distribution (in the range 0-1, with 1 corresponding to 100%) of the ratio f/Q at 4 different wavelengths (440, 510, 555 and 676 nm), as in Figure 9(b) of Morel and Gentili (1993). Values of f/Q have been estimated from Equation 4.
The radiative transfer simulations can also be used to assess variability in the transmission factor T by rearranging Equation 3. Mobley (1999) suggested a range between 0.50 - 0.57 for typical ocean waters and solar and sensor geometries. In this study, T was found to vary in the range 0.52 - 0.63 considering the Sun at the zenith and the sensor in the vertical direction,with the differences in ranges between the two studies presumably associated with the range of water conditions (and therefore IOPs) considered.
Overall, it is reasonable to suggest that the variability described by f/Q and T factors observed in this study are broadly consistent with previous studies.
rrs and IOP
This study investigates relationships between IOPs and both rrs(λ) and Rrs(λ) considering both wM and wG forms, and also considers both forward and inverse directions.
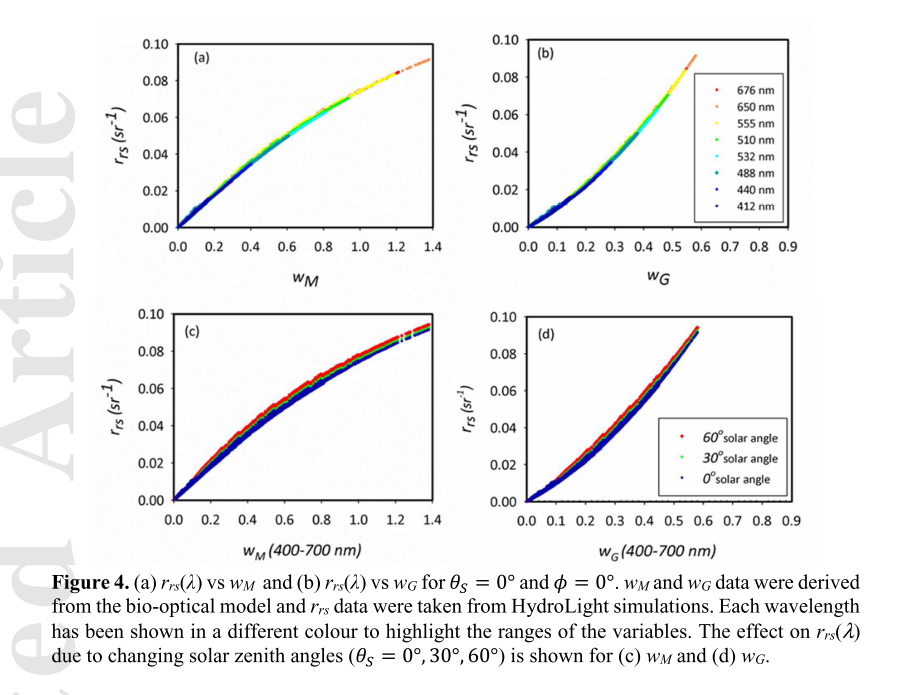
Plotting the HydroLight output rrs(λ) values against the input IOP terms, wM and wG,(Figure 4a and 4b), the relationships between rrs(λ) and either wM or wG are found to be non-linear but, crucially, monotonic.
Whereas the frequency distributions shown in Figure 3 do not offer any means of predicting a particular value of f/Q, Figure 4 suggests the possibility of establishing relationships between rrs and either wM or wG with strong predictive power in both the forward and reverse directions.
- both approaches (wM and wG) are equivalently valid
- dependence of the sub-surface remote sensing reflectance on wavelength (400 nm < λ < 700 nm) is minimal in Case 2 waters(in fig. a and fig.b, different wavelength almost in same curve)
- Changing the solar zenith angle (θs=0⁰; 30⁰; 60⁰) generates similar but non-identical nonlinear, monotonic relationships (Figures 4c and 4d) #### Rrs and IOP
- Rrs and w_m/w_G has analogous behavior compared to the corresponding case of sub-surface reflectance, with slightly less sensitivity to changing solar angles.
Determination of optimal IOP-rrs relationships
- significant divergence in the performance of each best- fit polynomial for low values of both wM and wG, and similarly when these parameters are derived from rrs(λ).
- performance for high values of rrs(λ), wM and wG is less sensitive to choice of polynomial
It is therefore important to consider performance over all relevant ranges of signal strength when attempting to establish a set of optimal empirical relationships.
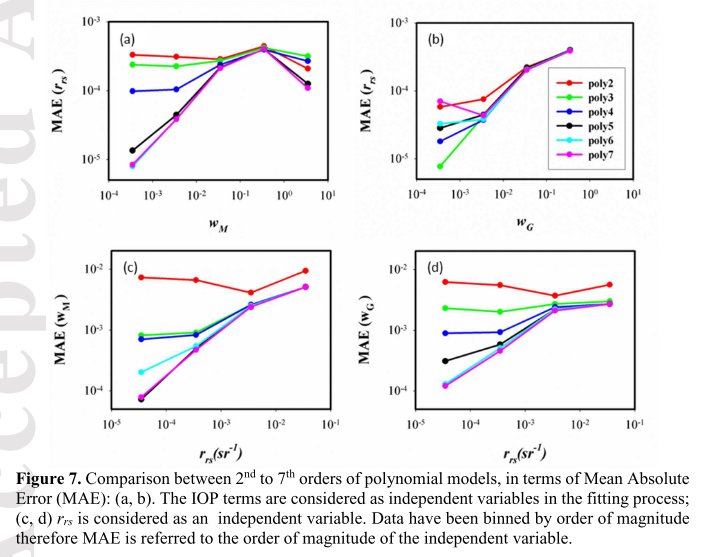
When estimating rrs(λ) from wM or wG (Figure 7a and 7b) it is possible to directly compare the two approaches because the derived term in both cases is rrs(λ). However, when comparing retrievals of bb(λ)/a(λ) and bb(λ)/[a(λ)+bb(λ)], it is important to bear in mind that the two variables are not numerically equivalent (Figure 7c and 7d).
- The results of this systematic exercise show that higher order polynomial models provide better performance than second order models to ensure similar goodness of fit across all decades of signal variation.
- recommended relationships in retrieving rrs(λ) from wM and vice versa are 6th and 5th order polynomials respectively (Figure 7a and 7c)
- A 3rd order polynomial is the suggested choice for retrieving rrs(λ) from wG, (Figure 7b),
- while a 6th order polynomial is needed for estimating wG from rrs(λ) (Figure 7d).
It is interesting to note that wM and wG approaches produce similar levels of MAE if sufficiently well-tuned polynomials are selected.
Overall there is no significant accuracy benefit of one form of IOP expression over the other.
The results of this exercise show that with suitably careful selection of empirical relationship, using wM or wG is broadly equivalent.
Determination of optimal IOP-Rrs relationshops
This part is almost the same with previous one. Here is the summary.
- higher order polynomials are suggested to ensure similar goodness of fit across all decades of signal variation, with the greatest impact occurring at small data values.
- the recommended relationships in retrieving Rrs(λ) from wM and vice versa are the 5th order polynomials in both case
- for retrieving Rrs(λ) from wG, a 4th order polynomial is the suggested choice (Figure 9b), while a 7th order polynomial is needed for estimating wG from Rrs(λ) (Figure 9d).
- Rrs(λ) can be expressed as a function of the absorption and backscattering coefficients of the water and it is equally valid to represent the IOPs using wM or wG.
- The limiting factor is not choice of either wM or wG, rather it is in selecting an appropriate formulation to represent variation the non-linear relationship with IOPs.
Comparison with previous studies
the existing established models for representing rrs(λ) (Gordon et al., 1988 and Lee et al., 2002, 2004) or Rrs(λ), based on low order polynomial relationships, are unable to fully account for the effect of multiple scattering which is particularly relevant in Case 2 waters (Wong et al., 2019).
Interestingly, the results presented above suggest that the performance of low-order polynomials tends to be worst for clear waters. It is clear from this analysis that higher order polynomials are generally necessary in order to achieve optimal performance across the full range of natural variability.
Poly5 model is very close to the version of Gordon’s model with coefficients suggested by Lee et al. (2002) which was intended to be applicable to both Case 1 and Case 2 waters.
Applying the Wong et al. (2019) approach to our data set presents smaller MAEs for lower values of wG, but higher MAE for higher values of wG.
It is important to note that the family of curve models shown in Figure 10a falls within the 95% confidence bounds of the proposed Poly5 relationship at the high end of the range (Figure 10c) while the 95% confidence bounds at the low end (Figure 10d) are an order of magnitude greater than the MAE differences between the various proposed relationships for the equivalent range in Figure 10b.
Discussion and conclusion
In this paper
a series of radiative transfer simulations across a very broad range of optical conditions has been conducted using the HydroLight RT code.
Input IOPs have been supplied through a linear spectral bio-optical model, varying the concentrations of in-water optical constituents across a wide range of concentrations to simulate natural variability
The resulting set of synthetic above and below surface reflectances have enabled investigation of relationships with IOPs expressed as either wM or wG.
The results demonstrate that the relationship between IOPs and either rrs or Rrs are highly predictable and can be well modelled by a non-linear but monotonic curve, which is not significantly wavelength dependent for 400nm<λ<700nm.
However, it has been shown here that in order to achieve consistent levels of prediction performance across the broad range of optical coastal water conditions considered, it is generally necessary to consider higher order polynomial relationships.
Comparison of wM and wG variants demonstrate effectively equivalent performance: there is no immediate advantage or disadvantage to use of either form in coastal waters.
The general proposition that either combination of absorption and backscattering contains sufficient relevant information to both predict and interpret remote sensing signals.
There may be situations where future end users may have reason to prefer use of one form over another and this study suggests there is no reason to be concerned over either
Annotation
This is a very fundamental paper related to the relationship between IOP and AOP. Specifically, this paper examine two relationship, f/Q and polynomial. I do not tend to make a summary for this paper all.
One thing I can learn from this paper is that how f/Q and polynomial effected by the environment. f/Q is mainly influenced by the water constitution, and small influenced by the sun angles, viewing geometries and solar zenith. It is in the range of 0.075 – 0.12.
For the relationship between rrs and IOP, the author examined different order of polynimal. The poly5 the author used seems slightly better than Lee 02 and Wong 2019, but the author said that this conclusion might be only true in the area they collected data. The poly5 is difficult to solve in the inversion problem, but I can try it in the reversion problem.
One interested thing is that the author use SIOP to generate IOP dataset. I'm wondering what could influence SIOP.
Algorithm to derive inherent optical properties from remote sensing reflectance in turbid and eutrophic lakes
10.1364/ao.58.008549
This paper is just to explore the failure and effort could do to improve QAA. So I haven't read it totally.
There are several things need to be noticed in this algorithm.
This paper changed the refferenced band to 750
First use emprical method to estimated ap750, and treat it as a constant value. Here is use ad750 from other paper
Then use analytical to built bbp750
Then an optimized parameter to get Y, the power exponent of bop shape
Then retrieve \(a_{nw}\), non-water absorption.
At last it retrieve \(a_{ph}\) first, then get\(a_{dg}\)
The most important contribution I think is 2 4 6
Modeling the remote-sensing reflectance of highly turbid waters
This paper acutually similar with the first one I read. He made a ploy4 model from IOP to rrs
Variability in the chlorophyll-specific absorption coefficients of natural phytoplankton: Analysis and parameterization
https://doi.org/10.1029/95JC00463
I finally know how band shifting using that equation to estimate \(a_{ph}\) at different wavelength.
Actually I think I need to check the SIOP paper Ramírez- Pérez et al. (2018), I really think.
In this paper, the author parameteration the app spectra shape by the following formula: \[ a_{ph}^{*}(\lambda)=A(\lambda)*CHL^{-B(\lambda)} \] Although in the table they attached, they found in some wavelength the r^2 is relative low, they still use this.
Substitute the SIOP by IOP, we can get another form of the former equation: \[ a_{ph}(\lambda)=A(\lambda)*CHL^{1-B(\lambda)} \]
After using QAA, we can got \(a_{ph}(443)\)
So for \(a_{ph}(443)\), we can know that \[ a_{ph}(443)=A(443)*CHL^{1-B(443)} \] Just divide these two equations.
And maybe I can found some other parameteration in coastal area for a ph spectra shape.
R(0-,λ) (nondim), defined as the ratio of the upwards to downwards planar irradiances,R(0-,λ)= Eu(0-,λ)/ Ed(0-,λ);Q=Eu(0-,λ)/Lu(0-,λ);so Lu(0-,λ)=Eu(0-,λ)/Q, substitute and get↩︎
The detailed information about phytoplankton fluorescence is in the Book 'Real-time Coastal Observing Systems for Marine Ecosystem Dynamics and Harmful Algal Blooms', Chapter 7, 'Phytoplankton fluorescence: theory, current literature and in situ measurement'↩︎