tensorflow基础

Posted on In Word count in article: 5.8k Reading time ≈ 21 mins.

开始炼丹的第二天

一个简单的神经网络搭建流程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import tensorflow as tf
mnist = tf.keras.datasets.mnist

(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(10, activation='softmax')
])

model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])
model.fit(x_train, y_train, epochs=5)

model.evaluate(x_test,  y_test, verbose=2)

产出的结果

1
2
3
4
5
6
7
8
9
10
11
12
Epoch 1/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.2962 - accuracy: 0.9155
Epoch 2/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.1420 - accuracy: 0.9581
Epoch 3/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.1064 - accuracy: 0.9672
Epoch 4/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.0885 - accuracy: 0.9730
Epoch 5/5
1875/1875 [==============================] - 3s 2ms/step - loss: 0.0749 - accuracy: 0.9765
313/313 - 0s - loss: 0.0748 - accuracy: 0.9778
[0.07484959065914154, 0.9778000116348267]

来看一下这个简单的神经网络的结构

x_train, x_test = x_train / 255.0, x_test / 255.0 是因为minist这个数据集是0-255的，做了规范化。

tf.keras.models.Sequential 则是一个计算的连接器，意思就是这个网络由下面这几步骤连接起来，按照顺序进行计算。

该网络的第一层 tf.keras.layers.Flatten 将图像格式从二维数组（28 x 28 像素）转换成一维数组（28 x 28 = 784 像素）。将该层视为图像中未堆叠的像素行并将其排列起来。该层没有要学习的参数，它只会重新格式化数据

展平像素后，网络会包括两个 tf.keras.layers.Dense 层的序列。它们是密集连接或全连接神经层。第一个 Dense 层有 128 个节点（或神经元）。第二个（也是最后一个）层会返回一个长度为 10 的 logits 数组。每个节点都包含一个得分，用来表示当前图像属于 10 个类中的哪一类。

这里面的Dropout则是一个正则化的trick，用来放置过拟合。Dropout的意思是：每次训练时随机忽略一部分神经元，这些神经元dropped-out了。换句话讲，这些神经元在正向传播时对下游的启动影响被忽略，反向传播时也不会更新权重。

神经网络的所谓“学习”是指，让各个神经元的权重符合需要的特性。不同的神经元组合后可以分辨数据的某个特征。每个神经元的邻居会依赖邻居的行为组成的特征，如果过度依赖，就会造成过拟合。如果每次随机拿走一部分神经元，那么剩下的神经元就需要补上消失神经元的功能，整个网络变成很多独立网络（对同一问题的不同解决方法）的合集。。意思就是在训练完第一个Dense之后，去掉20%的神经元来训练下一个Dense。相当于手动设置了一部分可能出错的神经元，用其他神经元来纠错。

model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])

这个是模型的编译。需要添加三个东西。

  • 损失函数 - 用于测量模型在训练期间的准确率。您会希望最小化此函数，以便将模型“引导”到正确的方向上。
  • 优化器 - 决定模型如何根据其看到的数据和自身的损失函数进行更新。
  • 指标 - 用于监控训练和测试步骤。以下示例使用了准确率，即被正确分类的图像的比率

损失函数和指标是两个因为目的不同而分开的东西。

损失函数存在的意义是在优化参数中需要最小化的一个函数，它存在的目的是优化模型的参数，当这个值最小的时候模型最好，一般需要求导或者做gradiant之类的。。而指标则是我们关心的评价。

举个例子，在回归中，MSE既可以是损失函数也可以是指标，但是R^2就不一定能作为损失函数使用，因为R2越大模型越好。

在分类问题中，我们可能只关注Accuracy（准确率Precision（精准率）Recall（召回率）ROC-AUC P-R曲线里面的某一项指标，但是这些指标一个可能是算起来困难花费时间，另一个是可能和R2有同样地问题，所以我们用的是交叉熵之类的。

具体的可以看这里

后面就很熟悉了。唯一一个之前没见过的东西就是 verbose=2

  • verbose: 'auto', 0, 1, or 2. Verbosity mode. 0 = silent, 1 = progress bar, 2 = one line per epoch. 'auto' defaults to 1 for most cases, but 2 when used with ParameterServerStrategy. Note that the progress bar is not particularly useful when logged to a file, so verbose=2 is recommended when not running interactively (eg, in a production environment).

所以看一眼输出

Epoch 5/5 1875/1875 [==============================] - 3s 2ms/step - loss: 0.0749 - accuracy: 0.9765 313/313 - 0s - loss: 0.0748 - accuracy: 0.9778

这种类似的是因为我们verbose=2之后输出的在训练集上面的结果

[0.07484959065914154, 0.9778000116348267]这个则是在测试集上面的

回归

大部分流程和前面一样，不再具体解释，例子来自于这里

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import pathlib

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns

import tensorflow as tf

from tensorflow import keras
from tensorflow.keras import layers
....#做了一些数据的清洗之后 我直接跳到模型的构建那里
def build_model():
  model = keras.Sequential([
    layers.Dense(64, activation='relu', input_shape=[len(train_dataset.keys())]),
    layers.Dense(64, activation='relu'),
    layers.Dense(1)
  ])

  optimizer = tf.keras.optimizers.RMSprop(0.001)

  model.compile(loss='mse',
                optimizer=optimizer,
                metrics=['mae', 'mse'])
  return model
model = build_model()

因为输出的是单独一个值，所以最后一层只有一个神经元。这个build model相当于一个生成model的函数。

在生成完模型之后可以看一下模型的简单描述

1
2
model.summary()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense (Dense)                (None, 64)                640       
_________________________________________________________________
dense_1 (Dense)              (None, 64)                4160      
_________________________________________________________________
dense_2 (Dense)              (None, 1)                 65        
=================================================================
Total params: 4,865
Trainable params: 4,865
Non-trainable params: 0
_________________________________________________________________
1
2
3
4
5
6
7
8
9
10
11
12
# 通过为每个完成的时期打印一个点来显示训练进度
class PrintDot(keras.callbacks.Callback):
  def on_epoch_end(self, epoch, logs):
    if epoch % 100 == 0: print('')
    print('.', end='')

EPOCHS = 1000

history = model.fit(
  normed_train_data, train_labels,
  epochs=EPOCHS, validation_split = 0.2, verbose=0,
  callbacks=[PrintDot()])

callbacks是每个epochs结束的时候执行的函数。

validation则是搞一个交叉验证。

history对象则可以可视化模型的训练进度。

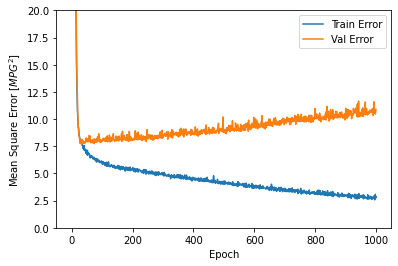
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def plot_history(history):
  hist = pd.DataFrame(history.history)
  hist['epoch'] = history.epoch

  plt.figure()
  plt.xlabel('Epoch')
  plt.ylabel('Mean Abs Error [MPG]')
  plt.plot(hist['epoch'], hist['mae'],
           label='Train Error')
  plt.plot(hist['epoch'], hist['val_mae'],
           label = 'Val Error')
  plt.ylim([0,5])
  plt.legend()

  plt.figure()
  plt.xlabel('Epoch')
  plt.ylabel('Mean Square Error [$MPG^2$]')
  plt.plot(hist['epoch'], hist['mse'],
           label='Train Error')
  plt.plot(hist['epoch'], hist['val_mse'],
           label = 'Val Error')
  plt.ylim([0,20])
  plt.legend()
  plt.show()


plot_history(history)
png
png

该图表显示在约100个 epochs 之后误差非但没有改进，反而出现恶化。 让我们更新 model.fit 调用，当验证值没有提高上是自动停止训练。 我们将使用一个 EarlyStopping callback 来测试每个 epoch 的训练条件。如果经过一定数量的 epochs 后没有改进，则自动停止训练。

你可以从这里学习到更多的回调。

1
2
3
4
5
6
7
8
9
model = build_model()

# patience 值用来检查改进 epochs 的数量
early_stop = keras.callbacks.EarlyStopping(monitor='val_loss', patience=10)
#即如果在10个训练后没有改进，就停止
history = model.fit(normed_train_data, train_labels, epochs=EPOCHS,
                    validation_split = 0.2, verbose=0, callbacks=[early_stop, PrintDot()])

plot_history(history)

过拟合和欠拟合

这一节开始就是英语了

依然是省略了一些前期处理

防止过度拟合的最简单方法是以一个小模型开始。一个具有少量可学习参数的模型（由层数和每层的单元数决定）。在深度学习中，一个模型中的可学习参数的数量通常被称为模型的 "容量"。

直观地说，一个拥有更多参数的模型将拥有更多的 "记忆能力"，因此能够轻易地在训练样本和它们的目标之间学习一个完美的类似字典的映射，这种映射没有任何泛化能力，但在对以前未见过的数据进行预测时，这将毫无用处。

永远记住这一点：深度学习模型往往善于拟合训练数据，但真正的挑战是泛化，而不是拟合。

另一方面，如果网络的记忆资源有限，它将无法轻易学习映射。为了使其损失最小化，它将不得不学习具有更多预测能力的压缩表征。同时，如果你让你的模型太小，它将难以适应训练数据。在 "容量太大 "和 "容量不足 "之间存在着一种平衡。

不幸的是，没有神奇的公式来确定你的模型的正确大小或架构（就层数而言，或每层的正确大小）。你将不得不使用一系列不同的架构进行试验。

为了找到一个合适的模型大小，最好从相对较少的层和参数开始，然后开始增加层的大小或增加新的层，直到你看到验证损失的回报递减。

接下来将从一个只使用密集连接层（tf.keras.layer.Dense）的简单模型开始作为基线，然后创建更大的模型，并进行比较。

训练过程

一般来说学习率越小效果越好,这个不难理解，我们可以利用tf.keras.optimizers.schedules来随着时间减少学习率

1
2
3
4
5
6
7
8
lr_schedule = tf.keras.optimizers.schedules.InverseTimeDecay(
  0.001,
  decay_steps=STEPS_PER_EPOCH*1000,
  decay_rate=1,
  staircase=False)

def get_optimizer():
  return tf.keras.optimizers.Adam(lr_schedule)

这个函数会双曲线的来减少学习率，比如，第1000epochs会降低到一半，两千会到1/3。具体的公式是

1
2
3
4
5
6
7
8
9
tf.keras.optimizers.schedules.InverseTimeDecay(
    initial_learning_rate, decay_steps, decay_rate, staircase=False, name=None
)#这是参数
#这是默认的函数（staircase=False）
def decayed_learning_rate(step):
  return initial_learning_rate / (1 + decay_rate * step / decay_step)
  #这是另一个函数（staircase=True）
def decayed_learning_rate(step):
  return initial_learning_rate / (1 + decay_rate * floor(step / decay_step))

下一步则是加入tf.keras.callbacks.EarlyStopping来避免训练太久。

1
2
3
4
5
6
def get_callbacks(name):
  return [
    tfdocs.modeling.EpochDots(),
    tf.keras.callbacks.EarlyStopping(monitor='val_binary_crossentropy', patience=200),
    tf.keras.callbacks.TensorBoard(logdir/name),
  ]

这里EarlyStopping关注的是val_binary_crossentropy，而不是val_loss，区别在后面会讲到。

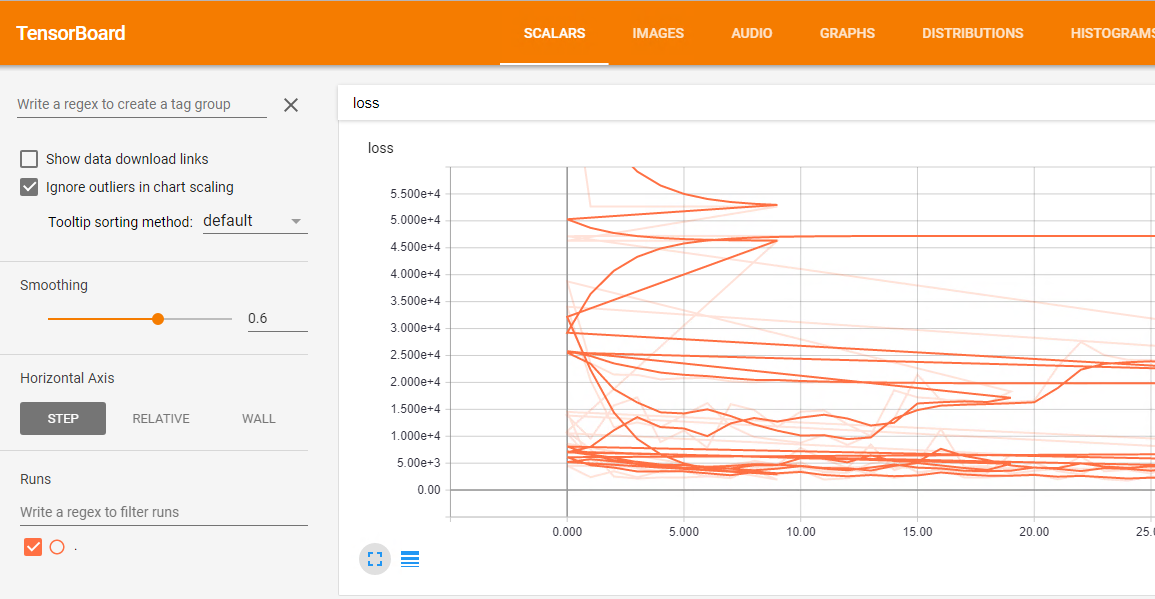
tf.keras.callbacks.TensorBoard则会直接显示一些定义好的metrics给你看，就像这样，具体的等后面看一下。

How to use Keras TensorBoard callback for grid search - Stack Overflow

然后利用Model.compile和Model.fit来构建一个网络。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def compile_and_fit(model, name, optimizer=None, max_epochs=10000):
  if optimizer is None:
    optimizer = get_optimizer()
  model.compile(optimizer=optimizer,
                loss=tf.keras.losses.BinaryCrossentropy(from_logits=True),
                metrics=[
                  tf.keras.losses.BinaryCrossentropy(
                      from_logits=True, name='binary_crossentropy'),
                  'accuracy'])

  model.summary()

  history = model.fit(
    train_ds,
    steps_per_epoch = STEPS_PER_EPOCH,
    epochs=max_epochs,
    validation_data=validate_ds,
    callbacks=get_callbacks(name),
    verbose=0)
  return history

我们从一个小模型来开始训练

1
2
3
4
5
6
tiny_model = tf.keras.Sequential([
    layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
    layers.Dense(1)
])
size_histories = {}
size_histories['Tiny'] = compile_and_fit(tiny_model, 'sizes/Tiny')

输出为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 16)                464       
                                                                 
 dense_1 (Dense)             (None, 1)                 17        
                                                                 
=================================================================
Total params: 481
Trainable params: 481
Non-trainable params: 0
_________________________________________________________________

Epoch: 0, accuracy:0.4896,  binary_crossentropy:0.8395,  loss:0.8395,  val_accuracy:0.5070,  val_binary_crossentropy:0.7700,  val_loss:0.7700,  
....................................................................................................
Epoch: 100, accuracy:0.6016,  binary_crossentropy:0.6240,  loss:0.6240,  val_accuracy:0.5910,  val_binary_crossentropy:0.6256,  val_loss:0.6256,  
....................................................................................................
Epoch: 200, accuracy:0.6269,  binary_crossentropy:0.6103,  loss:0.6103,  val_accuracy:0.6110,  val_binary_crossentropy:0.6151,  val_loss:0.6151,  
....................................................................................................
Epoch: 300, accuracy:0.6484,  binary_crossentropy:0.5984,  loss:0.5984,  val_accuracy:0.6340,  val_binary_crossentropy:0.6038,  val_loss:0.6038,  
....................................................................................................
Epoch: 400, accuracy:0.6584,  binary_crossentropy:0.5905,  loss:0.5905,  val_accuracy:0.6340,  val_binary_crossentropy:0.5993,  val_loss:0.5993,  
....................................................................................................
Epoch: 500, accuracy:0.6694,  binary_crossentropy:0.5860,  loss:0.5860,  val_accuracy:0.6410,  val_binary_crossentropy:0.5979,  val_loss:0.5979,  
....................................................................................................
Epoch: 600, accuracy:0.6684,  binary_crossentropy:0.5831,  loss:0.5831,  val_accuracy:0.6550,  val_binary_crossentropy:0.5960,  val_loss:0.5960,  
....................................................................................................
Epoch: 700, accuracy:0.6748,  binary_crossentropy:0.5810,  loss:0.5810,  val_accuracy:0.6510,  val_binary_crossentropy:0.5967,  val_loss:0.5967,  
....................................................................................................
Epoch: 800, accuracy:0.6707,  binary_crossentropy:0.5795,  loss:0.5795,  val_accuracy:0.6580,  val_binary_crossentropy:0.5965,  val_loss:0.5965,  
...........................

我们来画一下train test plot

1
2
3
plotter = tfdocs.plots.HistoryPlotter(metric = 'binary_crossentropy', smoothing_std=10)
plotter.plot(size_histories)
plt.ylim([0.5, 0.7])
1
(0.5, 0.7)
png

接着我们来换一个更大一点的模型来看看会不会好一点

1
2
3
4
5
6
7
small_model = tf.keras.Sequential([
    # `input_shape` is only required here so that `.summary` works.
    layers.Dense(16, activation='elu', input_shape=(FEATURES,)),
    layers.Dense(16, activation='elu'),
    layers.Dense(1)
])
size_histories['Small'] = compile_and_fit(small_model, 'sizes/Small')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
Model: "sequential_1"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense_2 (Dense)             (None, 16)                464       
                                                                 
 dense_3 (Dense)             (None, 16)                272       
                                                                 
 dense_4 (Dense)             (None, 1)                 17        
                                                                 
=================================================================
Total params: 753
Trainable params: 753
Non-trainable params: 0
_________________________________________________________________

Epoch: 0, accuracy:0.4877,  binary_crossentropy:0.7209,  loss:0.7209,  val_accuracy:0.4860,  val_binary_crossentropy:0.7025,  val_loss:0.7025,  
....................................................................................................
Epoch: 100, accuracy:0.6212,  binary_crossentropy:0.6148,  loss:0.6148,  val_accuracy:0.6200,  val_binary_crossentropy:0.6184,  val_loss:0.6184,  
....................................................................................................
Epoch: 200, accuracy:0.6657,  binary_crossentropy:0.5853,  loss:0.5853,  val_accuracy:0.6570,  val_binary_crossentropy:0.5949,  val_loss:0.5949,  
....................................................................................................
Epoch: 300, accuracy:0.6774,  binary_crossentropy:0.5750,  loss:0.5750,  val_accuracy:0.6720,  val_binary_crossentropy:0.5868,  val_loss:0.5868,  
....................................................................................................
Epoch: 400, accuracy:0.6838,  binary_crossentropy:0.5683,  loss:0.5683,  val_accuracy:0.6760,  val_binary_crossentropy:0.5859,  val_loss:0.5859,  
....................................................................................................
Epoch: 500, accuracy:0.6897,  binary_crossentropy:0.5632,  loss:0.5632,  val_accuracy:0.6720,  val_binary_crossentropy:0.5863,  val_loss:0.5863,  
....................................................................................................
Epoch: 600, accuracy:0.6946,  binary_crossentropy:0.5593,  loss:0.5593,  val_accuracy:0.6670,  val_binary_crossentropy:0.5883,  val_loss:0.5883,  
....................................................................................................
Epoch: 700, accuracy:0.6963,  binary_crossentropy:0.5558,  loss:0.5558,  val_accuracy:0.6730,  val_binary_crossentropy:0.5869,  val_loss:0.5869,  
....................................................................................................
Epoch: 800, accuracy:0.7006,  binary_crossentropy:0.5531,  loss:0.5531,  val_accuracy:0.6620,  val_binary_crossentropy:0.5894,  val_loss:0.5894,  
.........................

他还尝试了大的 更大的 最大的 来看Loss的图

png

在notebook里面可以查看TensorBoard

1
2
3
4
5
6
7
8
9
10
11
#docs_infra: no_execute

# Load the TensorBoard notebook extension
%load_ext tensorboard

# Open an embedded TensorBoard viewer
%tensorboard --logdir {logdir}/sizes

display.IFrame(
    src="https://tensorboard.dev/experiment/vW7jmmF9TmKmy3rbheMQpw/#scalars&_smoothingWeight=0.97",
    width="100%", height="800px")

具体效果看着挺不错的，不放图了。

保存和恢复模型

我去 居然是拿hdf5格式保存的 怪不得 OC-SMART是这个格式

那或许我可以试着读取一下

1
2
3
4
5
6
7
8
9
pip install pyyaml h5py  # Required to save models in HDF5 format
import os

import tensorflow as tf
from tensorflow import keras

print(tf.version.VERSION)
#省略一部分

在训练期间保存模型的话，用的是tf.keras.callbacks.ModelCheckpoint

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
checkpoint_path = "training_1/cp.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)

# Create a callback that saves the model's weights
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
                                                 save_weights_only=True,
                                                 verbose=1)

# Train the model with the new callback
model.fit(train_images, 
          train_labels,  
          epochs=10,
          validation_data=(test_images, test_labels),
          callbacks=[cp_callback])  # Pass callback to training

# This may generate warnings related to saving the state of the optimizer.
# These warnings (and similar warnings throughout this notebook)
# are in place to discourage outdated usage, and can be ignored.

这将创建一个 TensorFlow checkpoint 文件集合，这些文件在每个 epoch 结束时更新.

只要两个模型共享相同的架构，您就可以在它们之间共享权重。因此，当从仅权重恢复模型时，创建一个与原始模型具有相同架构的模型，然后设置其权重。

读取的方式则是

1
2
3
4
5
6
7
8
9
10
11
12
13
# Create a basic model instance
model = create_model()

# Evaluate the model
loss, acc = model.evaluate(test_images, test_labels, verbose=2)
print("Untrained model, accuracy: {:5.2f}%".format(100 * acc))

# Loads the weights
model.load_weights(checkpoint_path)

# Re-evaluate the model
loss, acc = model.evaluate(test_images, test_labels, verbose=2)
print("Restored model, accuracy: {:5.2f}%".format(100 * acc))

checkpoint 回调选项

回调提供了几个选项，为 checkpoint 提供唯一名称并调整 checkpoint 频率。

训练一个新模型，每五个 epochs 保存一次唯一命名的 checkpoint ：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Include the epoch in the file name (uses `str.format`)
checkpoint_path = "training_2/cp-{epoch:04d}.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)

batch_size = 32

# Create a callback that saves the model's weights every 5 epochs
cp_callback = tf.keras.callbacks.ModelCheckpoint(
    filepath=checkpoint_path, 
    verbose=1, 
    save_weights_only=True,
    save_freq=5*batch_size)

# Create a new model instance
model = create_model()

# Save the weights using the `checkpoint_path` format
model.save_weights(checkpoint_path.format(epoch=0))

# Train the model with the new callback
model.fit(train_images, 
          train_labels,
          epochs=50, 
          batch_size=batch_size, 
          callbacks=[cp_callback],
          validation_data=(test_images, test_labels),
          verbose=0)

手动保存权重

使用 Model.save_weights 方法手动保存权重。默认情况下，tf.keras（尤其是 save_weights）使用扩展名为 .ckpt 的 TensorFlow 检查点格式（保存在扩展名为 .h5 的 HDF5 中，保存和序列化模型指南中会讲到这一点）：

1
2
3
4
5
6
7
8
9
10
11
12
# Save the weights
model.save_weights('./checkpoints/my_checkpoint')

# Create a new model instance
model = create_model()

# Restore the weights
model.load_weights('./checkpoints/my_checkpoint')

# Evaluate the model
loss, acc = model.evaluate(test_images, test_labels, verbose=2)
print("Restored model, accuracy: {:5.2f}%".format(100 * acc))

HDF5 格式

Keras使用 HDF5 标准提供了一种基本的保存格式。

1
2
3
4
5
6
7
# Create and train a new model instance.
model = create_model()
model.fit(train_images, train_labels, epochs=5)

# Save the entire model to a HDF5 file.
# The '.h5' extension indicates that the model should be saved to HDF5.
model.save('my_model.h5')

现在，从该文件重新创建模型：

1
2
3
4
5
# Recreate the exact same model, including its weights and the optimizer
new_model = tf.keras.models.load_model('my_model.h5')

# Show the model architecture
new_model.summary()
1
2
loss, acc = new_model.evaluate(test_images, test_labels, verbose=2)
print('Restored model, accuracy: {:5.2f}%'.format(100 * acc))

限制

与 SavedModel 格式相比，H5 文件不包括以下两方面内容：

  • 通过 model.add_loss() 和 model.add_metric() 添加的外部损失和指标不会被保存（这与 SavedModel 不同）。如果您的模型有此类损失和指标且您想要恢复训练，则您需要在加载模型后自行重新添加这些损失。请注意，这不适用于通过 self.add_loss() 和 self.add_metric() 在层内创建的损失/指标。只要该层被加载，这些损失和指标就会被保留，因为它们是该层 call 方法的一部分。
  • 已保存的文件中不包含自定义对象（如自定义层）的计算图。在加载时，Keras 需要访问这些对象的 Python 类/函数以重建模型。请参阅自定义对象。

超参数调节

Keras Tuner 是一个库，可帮助您为 TensorFlow 程序选择最佳的超参数集。为您的机器学习 (ML) 应用选择正确的超参数集，这一过程称为超参数调节或超调。

超参数是控制训练过程和 ML 模型拓扑的变量。这些变量在训练过程中保持不变，并会直接影响 ML 程序的性能。超参数有两种类型：

  1. 模型超参数：影响模型的选择，例如隐藏层的数量和宽度
  2. 算法超参数：影响学习算法的速度和质量，例如随机梯度下降 (SGD) 的学习率以及 k 近邻 (KNN) 分类器的近邻数

在本教程中，您将使用 Keras Tuner 对图像分类应用执行超调。

直接跳过一堆

定义模型

构建用于超调的模型时，除了模型架构之外，还要定义超参数搜索空间。您为超调设置的模型称为超模型。

您可以通过两种方式定义超模型：

  • 使用模型构建工具函数
  • 将 Keras Tuner API 的 HyperModel 类子类化

您还可以将两个预定义的 HyperModel 类（HyperXception 和 HyperResNet）用于计算机视觉应用。

在本教程中，您将使用模型构建工具函数来定义图像分类模型。模型构建工具函数将返回已编译的模型，并使用您以内嵌方式定义的超参数对模型进行超调。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def model_builder(hp):
  model = keras.Sequential()
  model.add(keras.layers.Flatten(input_shape=(28, 28)))

  # Tune the number of units in the first Dense layer
  # Choose an optimal value between 32-512
  hp_units = hp.Int('units', min_value=32, max_value=512, step=32)
  model.add(keras.layers.Dense(units=hp_units, activation='relu'))
  model.add(keras.layers.Dense(10))

  # Tune the learning rate for the optimizer
  # Choose an optimal value from 0.01, 0.001, or 0.0001
  hp_learning_rate = hp.Choice('learning_rate', values=[1e-2, 1e-3, 1e-4])

  model.compile(optimizer=keras.optimizers.Adam(learning_rate=hp_learning_rate),
                loss=keras.losses.SparseCategoricalCrossentropy(from_logits=True),
                metrics=['accuracy'])

  return model

实例化调节器并执行超调

实例化调节器以执行超调。Keras Tuner 提供了四种调节器：RandomSearch、Hyperband、BayesianOptimization 和 Sklearn。在本教程中，您将使用 Hyperband 调节器。

要实例化 Hyperband 调节器，必须指定超模型、要优化的 objective 和要训练的最大周期数 (max_epochs)。

1
2
3
4
5
6
tuner = kt.Hyperband(model_builder,
                     objective='val_accuracy',
                     max_epochs=10,
                     factor=3,
                     directory='my_dir',
                     project_name='intro_to_kt')

Finetune

在本教程中，您将学习如何使用迁移学习通过预训练网络对猫和狗的图像进行分类。

预训练模型是一个之前基于大型数据集（通常是大型图像分类任务）训练的已保存网络。您可以按原样使用预训练模型，也可以使用迁移学习针对给定任务自定义此模型。

用于图像分类的迁移学习背后的理念是，如果一个模型是基于足够大且通用的数据集训练的，那么该模型将有效地充当视觉世界的通用模型。随后，您可以利用这些学习到的特征映射，而不必通过基于大型数据集训练大型模型而从头开始。

在此笔记本中，您将尝试通过以下两种方式来自定义预训练模型：

  1. 特征提取：使用先前网络学习的表示从新样本中提取有意义的特征。您只需在预训练模型上添加一个将从头开始训练的新分类器，这样便可重复利用先前针对数据集学习的特征映射。

您无需（重新）训练整个模型。基础卷积网络已经包含通常用于图片分类的特征。但是，预训练模型的最终分类部分特定于原始分类任务，随后特定于训练模型所使用的类集。

  1. 微调：解冻已冻结模型库的一些顶层，并共同训练新添加的分类器层和基础模型的最后几层。这样，我们便能“微调”基础模型中的高阶特征表示，以使其与特定任务更相关。

您将遵循通用的机器学习工作流。

  1. 检查并理解数据
  2. 构建输入流水线，在本例中使用 Keras ImageDataGenerator
  3. 构成模型
    • 加载预训练的基础模型（和预训练权重）
    • 将分类层堆叠在顶部
  4. 训练模型
  5. 评估模型

忽略一堆

从预训练卷积网络创建基础模型

您将根据 Google 开发的 MobileNet V2 模型来创建基础模型。此模型已基于 ImageNet 数据集进行预训练，ImageNet 数据集是一个包含 140 万个图像和 1000 个类的大型数据集。ImageNet 是一个研究训练数据集，具有各种各样的类别，例如 jackfruit 和 syringe。此知识库将帮助我们对特定数据集中的猫和狗进行分类。

首先，您需要选择将 MobileNet V2 的哪一层用于特征提取。最后的分类层（在“顶部”，因为大多数机器学习模型的图表是从下到上的）不是很有用。相反，您将按照常见做法依赖于展平操作之前的最后一层。此层被称为“瓶颈层”。与最后一层/顶层相比，瓶颈层的特征保留了更多的通用性。

首先，实例化一个已预加载基于 ImageNet 训练的权重的 MobileNet V2 模型。通过指定 include_top=False 参数，可以加载不包括顶部分类层的网络，这对于特征提取十分理想

1
2
3
4
5
# Create the base model from the pre-trained model MobileNet V2
IMG_SHAPE = IMG_SIZE + (3,)
base_model = tf.keras.applications.MobileNetV2(input_shape=IMG_SHAPE,
                                               include_top=False,
                                               weights='imagenet')

回到我自己的问题上

我现在是属于要用H5的那个，那么 首先我需要自己重新创建一个模型。

先补一下MLP

然后我也手动测试出了模型结构 下一个问题就是 怎么给Weight和Bias赋值

image-20220222222953159

好简单。。。只要肯查源码，什么都不是问题

这么写的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Fmodel.add(Dense(100, input_shape=(7,),activation='relu',
                 kernel_initializer=keras.initializers.Constant(np.array(f['Weights']['Layer1'])),
                bias_initializer=keras.initializers.Constant(np.array(f['Bias']['Layer1']))))

Fmodel.add(Dense(75, activation='relu',
                 kernel_initializer=keras.initializers.Constant(np.array(f['Weights']['Layer2'])),
                bias_initializer=keras.initializers.Constant(np.array(f['Bias']['Layer2']))))
Fmodel.add(Dense(50, activation='relu',
                 kernel_initializer=keras.initializers.Constant(np.array(f['Weights']['Layer3'])),
                bias_initializer=keras.initializers.Constant(np.array(f['Bias']['Layer3']))))
Fmodel.add(Dense(25, activation='relu',
                 kernel_initializer=keras.initializers.Constant(np.array(f['Weights']['Layer4'])),
                bias_initializer=keras.initializers.Constant(np.array(f['Bias']['Layer4']))))

Fmodel.add(Dense(7, activation='linear',
                 kernel_initializer=keras.initializers.Constant(np.array(f['Weights']['Layer5'])),
                bias_initializer=keras.initializers.Constant(np.array(f['Bias']['Layer5']))))

为什么他们结果不太一样呢

自己一开始是把activation写错了 写成了relu 就是上面那个，后面改成了tanh 应该一样了啊

再次开启debug，然后发现从第一层开始就有问题了。

所以这个dense tanh到底是怎么计算的呢

Dense implements the operation: output = activation(dot(input, kernel) + bias) where activation is the element-wise activation function passed as the activation argument, kernel is a weights matrix created by the layer, and bias is a bias vector created by the layer (only applicable if use_bias is True). These are all attributes of Dense.

对于原来的代码

1
lastlayer=np.tanh(np.matmul(aphnn_weights[i],aphinput.transpose())+aphnn_bias[i])

np.matmul和dot都是一样的，矩阵乘法

啊搞定了

因为keras.initializers.Constant只能给所有的weight和bias赋一样的值，所以会有差别。

新的写法改成了

1
2
3
4
5
6
7
8
9
10
Fmodel.add(Dense(100, input_shape=(7,),activation='tanh',use_bias=True))
Fmodel.layers[0].set_weights([np.array(f['Weights']['Layer1']).T,np.array(f['Bias']['Layer1']).flatten()])
Fmodel.add(Dense(75, activation='tanh',use_bias=True)
Fmodel.layers[1].set_weights([np.array(f['Weights']['Layer2']).T,np.array(f['Bias']['Layer2']).flatten()])
Fmodel.add(Dense(50, activation='tanh',use_bias=True)
Fmodel.layers[2].set_weights([np.array(f['Weights']['Layer3']).T,np.array(f['Bias']['Layer3']).flatten()])
Fmodel.add(Dense(25, activation='tanh',,use_bias=True)
Fmodel.layers[3].set_weights([np.array(f['Weights']['Layer4']).T,np.array(f['Bias']['Layer4']).flatten()])
Fmodel.add(Dense(7, activation='linear',use_bias=True,use_bias=True)
Fmodel.layers[4].set_weights([np.array(f['Weights']['Layer5']).T,np.array(f['Bias']['Layer5']).flatten()])

终于搞定了 后面做个finetune就可以了

https://www.kaggle.com/c/tensorflow-great-barrier-reef

https://tensorflow.google.cn/api_docs/python/tf/keras/optimizers/schedules/InverseTimeDecay

https://stackoverflow.com/questions/44747343/keras-input-explanation-input-shape-units-batch-size-dim-etc

https://vimsky.com/examples/usage/python-tf.keras.layers.Dropout-tf.html

https://cnbeining.github.io/deep-learning-with-python-cn/4-advanced-multi-layer-perceptrons-and-keras/ch16-reduce-overfitting-with-dropout-regularization.html