广义加性模型

Posted on In Word count in article: 5.2k Reading time ≈ 19 mins.

广义加性模型

去年这个时候准备SRDP立项就看到了一堆用广义加性模型的例子，国内关于这个的资源实在太少了，大半年之后我才开始学习用这玩意。把自己找到的各种参考文献整理一下作为学习笔记发出来，给别人一个方便。

（吐槽一句关于机器学习，感觉就是一个生造的概念，我在这里就把所有的这些东西称为统计学习——应用统计学的方法，让机器自行学习规律，然后给出结果。)

线性模型简单、只管、便于理解，但是很多时候在实际情况中并不能满足线性的假设。这时有两种方法，一个是通过降低模型的复杂度和估计量的方差来改善模型，另一种方法就是改变线性假设。由第二种方法引出的就是广义加性模型。

GAM 广义相加模型Generalized additive model

项目 说明
概念 回归模型中部分或全部的自变量采用平滑函数，降低线性设定带来的模型风险，对模型的假定不严，如不需要假定自变量线性相关于因变量（线性或非线性都可以）。
方程 ，g是一个链接函数，y是独立变量,为未知的光滑函数,代替经典线性回归中的，对样本要求少，适用性广
参数估计方法 最小二乘法，极大似然法
检验 残差Pseduo系数(PCf)估计，PCf = 1 - RD / ND (RD残差偏差，ND 无效偏差)
分类 可加/非参数（Aditive/Nonparametric): 参数（Parametric): 半参数/部分线性（Semiparametric/Partial Linear）: 薄板样条（Thin-plate spline）：允许两个自变量里有交互作用
前提 如x1和x2并非独立而存在交互作用，则应设为Thin-plate spline: f(x1, x2)（之所以有这一项是因为广义加性模型假定各项之间是相互独立的，这样计算最后的期望的时候就可以把他们加起来，如果不是相互独立的，需要手动设置交叉相互作用项） 模型中不必每一项都是非线性的，如都非线性会出现计算量大、过拟合等问题，通过查看xi与y的是否存在线性关系来判断是否使用平滑函数。 要遵循统计学和操作中的注意事项
光滑函数 见”样条函数”
缺点 样条函数参数的不确定性使之不能直接用于预估新的数据
Q&A 如何确定光滑项？ 这是个比较哲学的问题（掐死吧！） 1.计算每一种可能性，然后使用拟合效果最好的那个（利用一些标准来衡量，例如AIC） 2.使用最能够反应数据产生过程的那一个模型

（参考http://blog.csdn.net/textboy/article/details/47277131）

样条函数函数

我理解的这个模型就是说，和之间是线性关系，这样就可以使用线性回归的计算方法和检验方法来得到结果了，然后是一个平滑函数。这里样条函数是啥…对我就是不明白这一点，网上查到的资料说是和三次样条插值的那个函数差不多，但是这样不就变成插值了吗摔。

先给自己一个存疑，留待日后解决，然后更详细的参考资料如下

http://blog.csdn.net/tongweiganglp/article/details/53422324

http://www.loyhome.com/%e2%89%aa%e7%bb%9f%e8%ae%a1%e5%ad%a6%e4%b9%a0%e7%b2%be%e8%a6%81the-elements-of-statistical-learning%e2%89%ab%e8%af%be%e5%a0%82%e7%ac%94%e8%ae%b0%ef%bc%88%e5%8d%81%e4%ba%8c%ef%bc%89/

mgcv manual

Generalized Additive Models:An inroduction with R

AIC BIC ROC与AUC

任何一个统计学方法都会有过拟合欠拟合的问题，在吴恩达的课程里给出来了一种比较直观的感性的判断方式（以后会整理的抱头鼠窜）在这里介绍另一类方法，通过一个评价的函数来p安短，这里给出其中三种：AIC、BIC和ROC与AUC

（其实还有交叉验证方法，在后一个吴老师课程里讲的非常详细我也会整理的抱头鼠窜）

AIC

AIC是衡量统计模型拟合优良性的一种标准，由日本统计学家赤池弘次在1974年提出，它建立在熵的概念上，提供了权衡估计模型复杂度和拟合数据优良性的标准。

通常情况下，AIC定义为：

其中k是模型参数个数，L是似然函数。从一组可供选择的模型中选择最佳模型时，通常选择AIC最小的模型。假设条件是模型的误差服从独立正态分布。 让n为观察数，RSS为剩余平方和,则AIC变为：

当两个模型之间存在较大差异时，差异主要体现在似然函数项，当似然函数差异不显著时，上式第一项，即模型复杂度则起作用，从而参数个数少的模型是较好的选择。

一般而言，当模型复杂度提高（k增大）时，似然函数L也会增大，从而使AIC变小，但是k过大时，似然函数增速减缓，导致AIC增大，模型过于复杂容易造成过拟合现象。目标是选取AIC最小的模型，AIC不仅要提高模型拟合度（极大似然），而且引入了惩罚项，使模型参数尽可能少，有助于降低过拟合的可能性。

BIC

BIC（Bayesian InformationCriterion）贝叶斯信息准则与AIC相似，用于模型选择，1978年由Schwarz提出。训练模型时，增加参数数量，也就是增加模型复杂度，会增大似然函数，但是也会导致过拟合现象，针对该问题，AIC和BIC均引入了与模型参数个数相关的惩罚项，BIC的惩罚项比AIC的大，考虑了样本数量，样本数量过多时，可有效防止模型精度过高造成的模型复杂度过高。

其中，k为模型参数个数，n为样本数量，L为似然函数，kln(n)惩罚项在维数过大且训练样本数据相对较少的情况下，可以有限避免出现维度灾难现象。

ROC与AUC-衡量分类器的好坏

二元分类器

二元分类器是指要输出(预测)的结果只有两种类别的模型。例如预测阳性/阴性，有病/没病，在银行信用评分模型中，也用来预测用户是否会违约，等等。

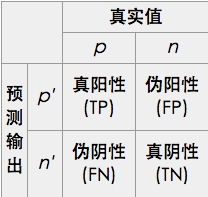
  既然是一种预测模型，则实际情况一定是有些结果猜对了，有些结果猜错了。因为二元分类器的预测结果有两种类别(以下以阴/阳为例)，对应其真实值，则会有以下四种情形:

Actual class
predict true positive false positive
class false negative true negative

img

图1.confusion matrix (混乱矩阵)

精确率是针对我们预测结果而言的，它表示的是预测为正的样本中有多少是对的。召回率是针对我们原来的样本而言的，它表示的是样本中的正例有多少被预测正确了。

当且仅当两者都高的时候，我们才可以说这种算法很NICE。在某些情况下我们可能要设定threshold来进行trade-off

  • 如果我们希望在很确信的情况下才告诉病人有cancer，也就是说不要给病人太多惊吓，我告诉你有cancer，你肯定有cancer；我告诉你没cancer，你也有可能有cancer，那么该情况下有：higher threshold，higher precision，lower recall
  • 如果我们不希望让病人错过提前治疗，与上例相反，就有：lower threshold，lower precision，higher recall

除此之外，还有另外一个评价标准来进行trade-off

越大越好

ROC空间与ROC曲线

在信号检测理论中，接收者操作特征曲线（receiver operating characteristic curve，或者叫ROC曲线）是一种座标图式的分析工具。  要了解ROC曲线，先要了解一下ROC空间，ROC空间是一个以伪阳性率(FPR, false positive rate)为X轴，真阳性率(TPR, true positive rate)为Y轴的二维坐标系所代表平面。

  • TPR: 真阳性率，所有阳性样本中(TP+FN)，被分类器正确判断为阳的比例。TPR = TP / (TP + FN) = TP / 所有真实值为阳性的样本个数
  • FPR: 伪阳性率，所有阴性样本中(FP+TN)，被分类器错误判断为阳的比例。FPR = FP / (FP + TN) = FP / 所有真实值为阴性的样本个数

  我们想象这样一种场景，接触阳性样本可以给我们带来“收益”，接触阴性样本则会给我们造成”成本”。并且如果我们接触样本中所有的阳性样本，我们的收益是1，接触样本中的所有阴性样本，我们的成本也是1。如果不接触样本，则既不产生收益也不产生成本。  自然的，如果不使用分类器，接触所有样本，则总的效益为1-1=0。现在让我们利用分类器来决定是否接触样本，分类器预测为阳，我们就去接触样本，分类器预测为阴，我们就不去接触。因为不接触样本不会产生收益或是成本，因此我们只需要看分类器预测为阳的样本。预测为阳的样本中，TP将产生 TPR 的收益， FP将产生FPR的成本。  那么一个分类器的分类效果就对应ROC空间里的一个点:

img

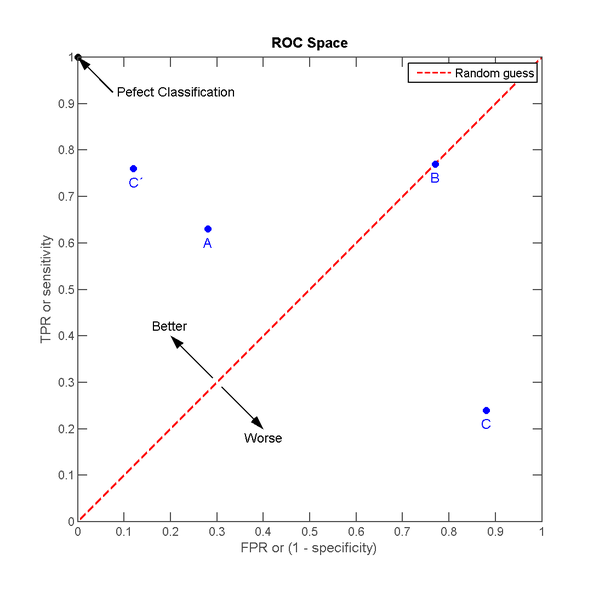
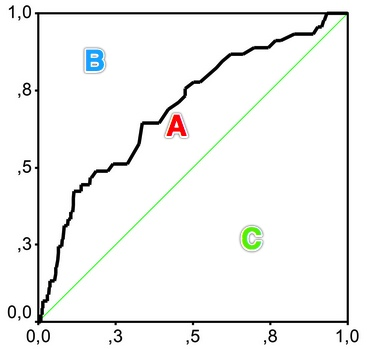
图2.ROC空间

A,B,C三个点可以分别代表三个不同的分类器对同样的样本做预测的结果。最好的方法是A，因为他的收益大于成本(TPR > FPR)，最差的是C(TPR < FPR)。中等的是B，相当于随机分类器。这里有趣的一点是若把C以(0.5, 0.5)为中点作一个镜像，得到C’， C’的效果比A要来的好。C’相当于一个做与C预测结果完全相反的分类器。  实际的应用当中，分类器还会给出它预测某个样本为阳的概率，并且有一个事先给定的门槛值(threshold)，概率高于threshold的就预测为阳性，低于threshold的就预测为阴性。假设以下是某个分类器对id为1-10的客户的分类结果:

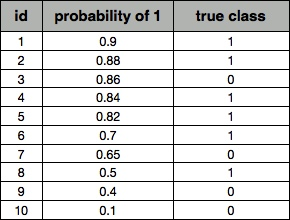
表1.分类器预测结果

img

其中probability of 1为分类器判断该样本为阳性的概率，true class为该样本的真实情况。  如果我们把threshold定位0.5，即去接触id为1~8的客户。此时

1
2
TPR = TP / 所有真实值为阳性的样本个数 = 6 / 6 = 1
FPR = FP / 所有真实值为阴性的样本个数 = 2 / 4 = 0.6

同理，如果我们把threshold定位0.8，即去接触id为1~5的客户。此时

1
2
TPR = TP / 所有真实值为阳性的样本个数 = 4 / 6 = 0.67
FPR = FP / 所有真实值为阴性的样本个数 = 1 / 4 = 0.25

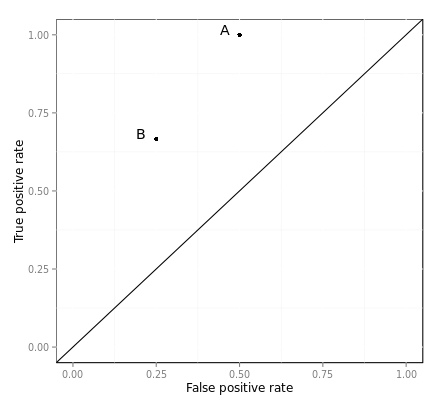
  这两个threshold分别对应ROC空间中的两个点A、B

img

图3.不同的threshold对应ROC空间中不同的点

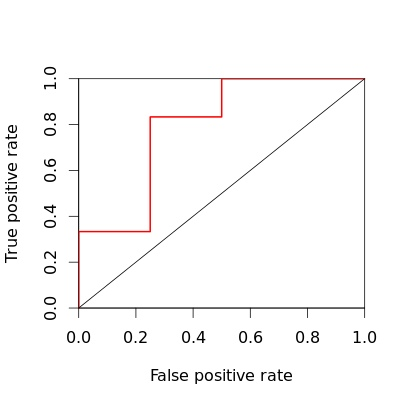
上面的例子当中，共有10笔预测数据，则一共有11种threshold的设定方法，每一个threshold对应ROC空间中的一个点，把这些点连接起来，就成了ROC曲线。

img

图4.ROC曲线

  这里因为数据量太少，所以曲线是一折一折的，数据量大的时候，看上去才像”曲线”。

AUC

(Area under the Curve of ROC) 曲线下面积

以下直接搬维基百科:

  • 因为是在1x1的方格里求面积，AUC必在0~1之间。
  • 假设threshold以上是阳性，以下是阴性；
  • 若随机抽取一个阳性样本和一个阴性样本，分类器正确判断阳性样本的值高于阴性样本之机率。(即前文当中把C做一个镜像变为C’)
  • 简单说：AUC值越大的分类器，正确率越高。

  从AUC判断分类器（预测模型）优劣的标准：

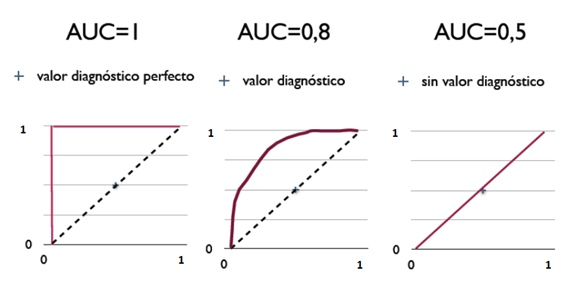
  • AUC = 1，是完美分类器，采用这个预测模型时，不管设定什么阈值都能得出完美预测。绝大多数预测的场合，不存在完美分类器。

  • 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。

  • AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。

  • AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测，因此不存在AUC < 0.5的情况。

    img

    图5.用AUC来衡量不同分类器的分类能力(更准确的说是排序能力)

    总结

    一个分类模型的分类结果的好坏取决于以下两个部分：

    1. 分类模型的排序能力(能否把概率高的排前面，概率低的排后面)
    2. threshold的选择

      使用AUC来衡量分类模型的好坏，可以忽略由于threshold的选择所带来的影响，因为实际应用中，这个threshold常常由先验概率或是人为决定的。

    补充：Gini coefficient

    在用SAS或者其他一些统计分析软件，用来评测分类器分类效果时，常常会看到一个叫做gini coefficient的东西，那么这个gini coefficient又是什么呢？gini系数通常被用来判断收入分配公平程度，具体请参阅wikipedia-基尼系数。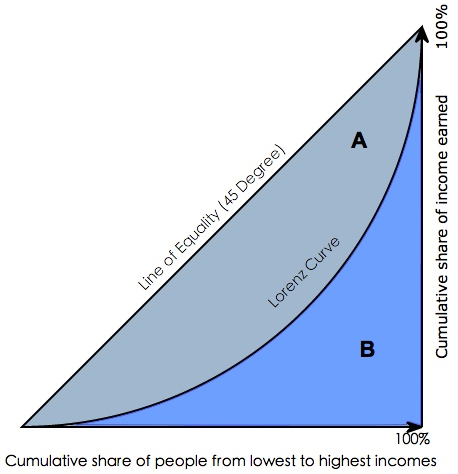img  图6.洛伦茨曲线与基尼系数

      Gini coefficient 是指绝对公平线(line of equality)和洛伦茨曲线(Lorenz Curve)围成的面积与绝对公平线以下面积的比例，即gini coefficient = A面积 / (A面积+B面积) 。

      用在评判分类模型的预测效力时，是指ROC曲线曲线和中线围成的面积与中线之上面积的比例。

    img  图7.Gini coefficient与AUC

    因此Gini coefficient与AUC可以互相转换：

    1
      
    1
    gini = A / (A + B) = (AUC - C) / (A + B) = (AUC -0.5) / 0.5 = 2*AUC - 1

参考 ：

http://blog.csdn.net/lfdanding/article/details/50732762?locationNum=8&fps=1

http://beader.me/2013/12/15/auc-roc/

R语言实现

R语言实现广义加性模型及相关函数

仅仅列出我最常用的几个 gam gam.check plot.gam predict.gam choose.k gam.selection

(给自己开了一个大坑啊，不知道能不能在生态学下课之前写完)

（看来是写不完了，要下课了…)

这一部分参考了manual和 R语言实现广义加性模型 Generalized Additive Models(GAM) 入门

1.实现和画图

R语言官网：http://www.r-project.org/

R语言软件下载：http://ftp.ctex.org/mirrors/CRAN/ 注：下载时点击 install R for the first time

下面进行一个简单的入门程序学习。

先新建一个txt，叫做 Rice_insect.txt，内容为：

选区_002

　　Adult为累计蛾量，Day为降雨持续天数，Precipitation为降雨量。

输入代码：

1
2
3
4
5
6
7
library(mgcv)      #加载mgcv软件包，因为gam函数在这个包里
Data <- read.delim("Rice_insect.txt")     #读取txt数据，存到Data变量中
Data <- as.matrix(Data)     #转为矩阵形式
#查看Data数据：Data，查看第2列：Data[,2]，第2行：Data[2,]

result1 <- gam(log(Adult) ~ s(Day))     #此时，Adult为相应变量，Day为解释变量
summary(result1)      #输出计算结果

　　此时可以看到：

Family: gaussian Link function: identity

Formula:log(Adult) ~ s(Day)

Parametric coefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) 7.9013 0.3562 22.18 4.83e-13 —Signif. codes: 0 ‘’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:edf Ref.df F p-values(Day) 1.713 2.139 0.797 0.473

R-sq.(adj) = 0.0471 Deviance explained = 14.3%GCV score = 2.6898 Scale est. = 2.2844 n = 18

Day的影响水平p-value=0.473，解释能力为14.3%，说明影响不明显。

其中，edf为自由度，理论上，当自由度接近1时，表示是线性关系；当自由度比1大，则表示为曲线关系。

接下来使用另一个解释变量Precipitation。输入代码：

1
2
result2 <- gam(log(Adult) ~ s(Precipitation))
summary(result2)

　　发现：

Family: gaussian Link function: identity

Formula:log(Adult) ~ s(Precipitation)

Parametric coefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) 7.9013 0.2731 28.94 1.87e-12 —Signif. codes: 0 ‘’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:edf Ref.df F p-value s(Precipitation) 5.022 6.032 2.561 0.0774 .—Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

R-sq.(adj) = 0.44 Deviance explained = 60.6%GCV score = 2.0168 Scale est. = 1.342 n = 18

此时p-value为0.0774，说明该因子在P<0.1水平下影响显著。（一般情况下p<0.05为显著。）

接下来画图：

1
plot(result2,se=T,resid=T,pch=16)

　　img

pch=16这个是图标的序号，比如改成17就是三角形了。

log(Adult)中的log是什么意思呢?

log是数据变换，取对数可以把大范围的数变成小范围的数，这在将几组相差太大的数据画在同一个坐标轴时特别有用，比如一组数据范围是1～10，第二组数据范围是10～100000000，要是不对第二组取常用对数，第一组在坐标轴上只是一点点，都看不到，对第二组取常用对数后，第二组范围变成1～8了，这样两组数据都能看到了。

下面尝试将两个变量同时作为解释变量。

1
result3<-gam(log(Adult)~s(Precipitation)+s(Day))

　　出错：Model has more coefficients than data

1
result3<-gam(log(Adult)~s(Precipitation,k=9)+s(Day,k=9)

　　k是什么？

　　k is the dimension of the basis used to represent the smooth term. If k is not specified then basis specific defaults are used.

K的最小值是3，最大值是17，为3、4的时候都是直线，说明太小了体现不出来，在不断增大的过程中发现，K越大，曲线原来越平滑，再大时，曲线就出现了一些弯曲，说明更精准了，再大时，图形就基本不变了，说明也没必要设那么大了。

再

1
summary(result3)

　　结果：

Family: gaussian Link function: identity

Formula:log(Adult) ~ s(Precipitation, k = 9) + s(Day, k = 9)

Parametric coefficients:Estimate Std. Error t value Pr(>|t|) (Intercept) 7.9013 0.2831 27.91 8.16e-12 —Signif. codes: 0 ‘’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Approximate significance of smooth terms:edf Ref.df F p-value s(Precipitation) 4.653 5.572 2.546 0.0848 .s(Day) 1.000 1.000 0.500 0.4939 —Signif. codes: 0 ‘’ 0.001 ‘’ 0.01 ‘’ 0.05 ‘.’ 0.1 ‘ ’ 1

R-sq.(adj) = 0.398 Deviance explained = 59.8%GCV score = 2.288 Scale est. = 1.4423 n = 18

2.其它函数

具体内容请查看manual

函数 描述 用法
gam.check 采用由gam（）生成的拟合的gam对象来产生关于拟合程序和结果的一些诊断信息。 缺省情况是产生4个残差图，关于光滑性选择优化的收敛的一些信息，以及运行基本维度选择是否足够的诊断测试。 应用于由gamm返回的gam对象时应注意解释结果。 gam.check(b,old.style=FALSE, type=c(“deviance”, “pearson”, “response”), k.sample=5000,k.rep=200, rep=0, level=.9, rl.col=2, rep.col=”gray80”, …)参数说明见后
predict.gam 采用由gam（）生成的拟合gam对象来给出一组新的用于模型协变量或用于模型拟合的原始值的预测值。 基于模型系数的后验分布，预测可以伴随着标准误差。 常规程序可以选择性地返回模型系数的矩阵，这个矩阵必须必须预先倍增（？？？），以便在所提供的协变量值处产生线性预测值的值：这对于从模型中获得的预测值获得置信区间是有用的（例如， 从平滑函数中衍生）以及R之外的查找表预测。 predict(object, newdata, type=”link”, se.fit=FALSE, terms=NULL, exclude=NULL, block.size=NULL, newdata.guaranteed=FALSE, na.action=na.pass,unconditional=FALSE,…)参数说明：object是预测出的模型，newdata是预测基于的自变量的值，注意一个是名字要和之前构建模型的名字一样，另一个是如果缺省，给出的结果是基于之前模型构建样本的因变量值，其余缺省即可

gam.check参数说明

参数 说明
b 由GAM模型产生的结果
old.style 如果改成true得到word2006版本的图像（黑人问号脸）
type 餐叉的类型，具体参见residuals.gam
k.sample 在这个k值水平上使用一个来自于样本的随机子集来测试
k.rep 多少次重新洗牌才能得到k测试的p值（黑人）
rep, level, rl.col, rep.col 在old.style为false时传递给qq.gam（）的参数，请参阅qq.gam().

剩余的图形参数请参见画图函数的参数

R实现AIC BIC ROC AUC

非常简单！

1
2
3
AIC(object, ..., k = 2)

BIC(object, ...)

ROChttp://blog.csdn.net/solo7773/article/details/8699693

AUC http://www.aichengxu.com/python/8900342.htme