The optics of backscattering

I need to understand the optics of backscattering to understand the strange 'bbp' calculted from Rrs and and.

Material mainly from IOCCG summer lecture 2018 and ocean optics web book.

Volume scattering function

VSF-geometry-600

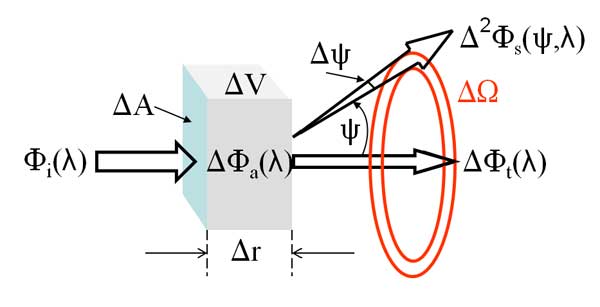
the fraction of incident power scattered out of the beam through an angle \(\psi\) into a solid angle \(\Delta\Omega\) (total radiance inside the cone)centered on \(\psi\), is \(\Delta^2\Phi_s(\psi,\lambda)/\Phi_i\).

If we change \(\Omega\) to \(\Omega+\Delta\Omega\), the increase part is inside the red ring,

The volume scattering function β(ψ,λ) is defined as the limit of this fraction as Δr→0 and ΔΩ→0:

image-00030505202530364

The physical meaning of VSF is

scattered intensity per unit incident irradiance per unit volume of water

Or

the differential scattering cross section per unit volume.

So the scattering is the integration of VSF over all direction \[ b(\lambda)=\int\beta(\psi,\lambda)d\Omega \] \(\Omega\) is the solid angle

https://www.youtube.com/watch?v=VmnkkWLwVsc

https://www.youtube.com/watch?v=gLfYTP4F23g

https://www.youtube.com/watch?v=RMJucQJ1NGo

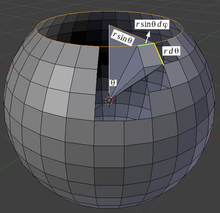\[ d\Omega=\frac{dA}{r^2}\\=\frac{d(rsin\theta d\psi)(rd\theta)}{r^2}\\=\frac{dr^2sin\theta d\theta d\psi}{r^2}\\=sin\theta d\theta d\psi \] By assuming azimuthal symmetry, this means it is a cone, the eq2 can be simplifed as : \[ d\Omega=\frac{dA}{r^2}\\ =\frac{d(2\pi r^2(1-cos\theta))}{r^2}\\ =2\pi sin \theta d\theta \]

\[ \therefore\\ b(\lambda)=\int\beta(\psi,\lambda)d\Omega\\ =2\pi\int_0^{\pi} sin(\theta)\beta(\theta,\lambda)d\theta\\ \]

The scattering is addictive

image-00030505220107010

There are some other scattering properties

image-00030505220204576

50% typically <3 to 4 deg

image-00030505221010160

Scattering components

Pure water

The best value of pure water scattering is

image-00030505224321192

detailed can check Lee lecture bases

Phytoplankton

image-00030506095901340

Particles

image-00030506100604399

image-00030506101019868

DDA is most popular one but only could compute very small size

Improve IGOM for larger size

Rayleigh cover very very small

Mie all size but homogeneous spheres

T-matrix is also popular

Measurement

I'm not very totally understand this process

But one thing I can now is that

The backscattering is the integration, but the measurement is a weighted sum

Interpretation and Application

image-00030506111348360

image-00030506111806825

Mie theory

Beam Attenuation

Unlike backscattering or total scattering, particle beam attenuation is almost a perfect powe law shape \[ c_p=a_p+b_p\\ =a_{ph}+a_{nap}+b_p \]

Not here this is \(b_p\), total scattering , not backscattering. Backscattering only contributed to almost one to two percent of total scattering.

In order to related to the backscattering that can be received by satellite, we need one bridge \(\hat{b}_{bp}\), defined as \[ \hat{b}_{bp}=\frac{b_{bp}}{b_{p}} \] The \(\hat{b}_{bp}\) almost same in different wavelength.

So the term u can be replaced as \[ u=\frac{b_b}{a+b_b}\\ =\frac{b_w+b_{bp}}{a_w+a_p+a_{CDOM}+b_w+b_{bp}}\\ =\frac{b_w+b_{p}*\hat{b}_{bp}}{a_w+a_p+a_{CDOM}+b_w+b_{p}*\hat{b}_{bp}}\\ =\frac{b_w+(c_p-a_p)*\hat{b}_{bp}}{a_w+a_p+a_{CDOM}+b_w+(c_p-a_p)*\hat{b}_{bp}}\\ \]