Correlation metrics
本科毕设就没搞懂的两个r现在终于弄明白了
大部分内容来自于维基百科
主要讲Brewin 2015里面用到的metrics
Pearson’s r
在统计学中,皮尔逊积矩相关系数(英语:Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs[1], 文章中常用r或Pearson’s r表示)用于度量两个变量X和Y之间的相关程度(线性相关),其值介于-1与1之间。
定义
两个变量之间的皮尔逊相关系数定义为两个变量的协方差除以它们标准差的乘积: $$ \rho_{X,Y}=\frac{cov(X,Y)}{\sigma_X\sigma_Y}=\frac{E[(X-\mu_x)(Y-\mu_Y)]}{\sigma_{X}\sigma{Y}} $$
这个是总体相关系数,对于我们抽样的样本,我们可以得到样本相关系数 $$ r=\frac{\sum_{i=1}^{n}(X_i-X)\sum_{i=1}^{n}(Y_i-Y)}{\sqrt{\sum_{n=1}^{n}}(X_i-\bar{X})^2\sqrt{\sum_{n=1}^{n}}(Y_i-\bar{Y})^2} $$
其中X̄代表样本平均值
数学特性
总体和样本皮尔逊系数的绝对值小于或等于1。如果样本数据点精确的落在直线上(计算样本皮尔逊系数的情况),或者双变量分布完全在直线上(计算总体皮尔逊系数的情况),则相关系数等于1或-1。皮尔逊系数是对称的:corr(X,Y) = corr(Y,X)。
皮尔逊相关系数有一个重要的数学特性是,因两个变量的位置和尺度的变化并不会引起该系数的改变,即它该变化的不变量 (由符号确定)。也就是说,我们如果把X移动到a + bX和把Y移动到c + dY,其中a、b、c和d是常数,并不会改变两个变量的相关系数(该结论在总体和样本皮尔逊相关系数中都成立)
与相关系数
这个是最容易混淆的,首先明确R2 ≠ r2并不一直成立,最简单的可以从计算方式来看。
决定系数(英语:coefficient of determination,记为R2或r2)在统计学中用于度量因变量的变异中可由自变量解释部分所占的比例,以此来判断统计模型的解释力。
对于简单线性回归而言,决定系数为样本相关系数的平方。[4]当加入其他回归自变量后,决定系数相应地变为多重相关系数的平方。
假设一数据集包括y1, ..., yn共n个观察值,相对应的模型预测值分别为f1, ..., fn。定义残差ei = yi − fi,平均观察值为 $$ \bar{y}=\frac{1}{n}\sum_{i=1}^{n}y_i, $$ 于是可以得到总平方和 SStot = ∑i(yi−ȳ)2, 回归平方和 SSreg = ∑i(fi−ȳ)2, 残差平方和 SSres = ∑i(yi − fi)2 = ∑iei2, 由此,决定系数可以定义为 $$ R^2=1-\frac{SS_{res}}{SS_{tot}} $$ 简单点说r计算是在xy之间,R^2计算是在y y_fit之间。
所以R^2的理论范围是( − ∞, 1],并不是[0,1]
只有对于线性回归的最小二乘拟合才有$\rho(x,y)=\pm\sqrt{R^2}$
证明如下 $$ \rho(x,y)=\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{n=1}^{n}}(x_i-\bar{x})^2\sqrt{\sum_{n=1}^{n}}(y_i-\bar{y})^2} $$
$$ \rho(\hat{y},y)=\frac{\sum_{i=1}^{n}(\hat{y}_i-\bar{y})(y_i-\bar{y})}{\sqrt{\sum_{n=1}^{n}}(\hat{y}_i-\bar{y})^2\sqrt{\sum_{n=1}^{n}}(y_i-\bar{y})^2}\\ =\frac{\beta_1\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\beta_1\sum_{n=1}^{n}}(x_i-\bar{x})^2\sqrt{\beta_1\sum_{n=1}^{n}}(y_i-\bar{y})^2}\\ =sgn(\beta_1)\frac{\sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{n=1}^{n}}(x_i-\bar{x})^2\sqrt{\sum_{n=1}^{n}}(y_i-\bar{y})^2}\\ =sgn(\beta_1)\rho(x,y) $$
在特殊情况下,带有截距项的线性最小二乘多元回归中,等于实测值
和拟合值
的相关系数的平方。
另一个特殊情况是,带有截距项的线性最小二乘简单回归中,等于自变量
和因变量
的相关系数的平方
主要来自https://www.zhihu.com/question/32021302
scikit-learn里的r2是R2
RMSE,Bias, uRMSE
这几个都是y和y_fit,很简单,直接上截图吧懒得写


Bias有时也用Relative bias或者MAPE
Slope and Intercept

Type-2用的是这个包https://github.com/OceanOptics/pylr2
我觉得没啥问题 一看就很专业
Log transfermation
主要是要搞明白这个
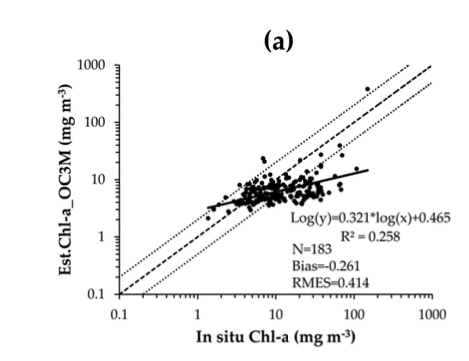
图里两条虚线分别是Y=2X和Y=X/2。
X轴每一个大tick代表的是log10(in situ Chla), Y轴代表的是log10(Chla OC3M),标注的数字是in situ Chla和Chla OC3M
这也是为啥 那条Regression line是Log(y)=a*log(x)+b。
调换一下 就是 y=x10^a + 10^b。
虽然X轴和Y轴标注的数字就是那个In situ Chla,但是实际上每一格对应的数字是1,2,3,4,标注的对应的是10^1, 10^2, 10^3, 10^4,这也是那个Minor tick会先大间隔后小间隔的原因。
但是y=2x和y=x/2这两条线代表的还是Chla OC3M=2 in situ Chla这种的情况
但是在Linear的里面这仨不是平行线,在这里平行了
是因为实质上 画的这两条线是log chla oc3m=log2 +login situ Chla
log2大概是0.3,对应的就是10