IOP inversion
This note is based on Lee 1998,1999,2002 and P. Werdell 2013
QAA
The reason for failure of QAA
After one year I found that I haven’t finish the note. I will try to finish this.
But before that I think I found the reason for the failure of QAA

Address: http://www.ioccg.org/groups/Software_OCA/QAA_v6_2014209.pdf
This is the whole process of QAA v6. Compared with the former one, the main update is in step2.
This is because in the first version, in the oligotrophic water, the aph is very low. Meanwhile the aCDOM has a very influence in the atotal at 55xnm. So the atotal is mainly determined by aw. As a result, lee used an emprical relationship from rrs to estimated atotal(55x). But in the coastal area, the atotal is dominated other constituents besides water, it make a lot of difference. It is also the reason that the update mainly happened in step2.
NIR base QAA
Some recent research use NIR wavelength for the step 2 as the non-water absorption at NIR is low.
Here is the ‘A blended inherent optical property algorithm for global satellite ocean color observations’.
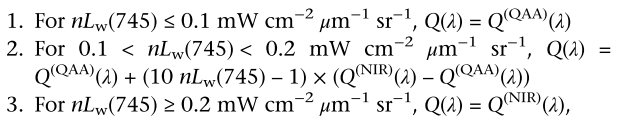

Another two is in Taihu.


QAA-750 is somewhat almost same with NIR-QAA, but QAA750-ap found that in Taihu, the ap750 sometime is still can’t negletable.
We don’t have ap763, I hope we can have that dataset later.
GIOP
This is another commly used Semi-analytical algorithm for IOP inversion.
This is the default algorithm of NASA IOP product
Introduction
- SAA always differentiations only in the assumputions employed to define the eigenvectors and in the mathematical methods applied to calculate the eigenvalues
- GIOP allows construction of different IOP models at runtime by selection from a wide assort-ment of published absorption and backscattering eigenvectors.
Method
Model Development
Lee et al 2002, Rrs to rrs $$ r_{rs}(\lambda,0^-)=\frac{R_{rs}(\lambda)}{0.52+1.7R_{rs}(\lambda)} $$ rrs to IOP rrs(λ,0−) = G1(λ)u(λ) + G2(λ)u(λ)2
$$ u(\lambda)=\frac{b_b{(\lambda)}}{a(\lambda)+b_b(\lambda)} $$
Common methods for estimating G?λ? include Gordon et al. [21], where G1 and G2 are spectrally fixed to 0.0949 and 0.0794 (see [7,23] for alternative coefficients), and the tabulated results ofMorel et al. [22], where G1 is estimated using solar and sensor geometries and an estimate of algal bio- mass and G2 is set to 0. GIOP supports all of these options.
IOP decomposition
each component can be expressed as the product of its concentration-specific absorption spectrum (eigenvector; a?) and its concentration or amplitude (eigenvalue; A): $$ a(\lambda)=a_w(\lambda)+\sum_{i=1}^{N}A_{ph}a_{ph}^{*}(\lambda)+\sum_{i=1}^{N}A_{d}a_{d}^{*}(\lambda)+\sum_{i=1}^{N}A_{g}a_{g}^{*}(\lambda) $$ Both ad*(λ) and ag*(λ) are commonly expressed as ad, g*(λ) = exp(−Sd, gλ) where Sd and Sg typically vary between 0.01 and 0.02 nm−1 in natural waters [24].
As the spectral shapes of NAP and CDOM absorption differ only in their exponential slopes, the two components are typically combined for satellite applications and Eq. (4) becomes
$$ a(\lambda)=a_w(\lambda)+\sum_{i=1}^{N}A_{ph}a_{ph}^{*}(\lambda)+\sum_{i=1}^{N}A_{dg}a_{dg}^{*}(\lambda) $$ For total backscattering $$ b_b(\lambda)=b_{bw}({\lambda})+\sum_{i=1}^NB_{bp}b_{bp}(\lambda) $$ Bbp provides the eigenvalue and a power function often represents the eigenvector: bbp*(λ) = λSbp where Sbp typically varies between −2 and 0 from small to large particles.
While commonly employed in the remote-sensing paradigm, we acknowledge the validity of the power function for b? bpλ remains debatable [25–27].
Using Rrsλ and eigenvectors as input, eigenvalues for absorption (A) and backscattering (B) can be estimated via linear or nonlinear least squares inversion of Eqs. (1)–(3).
Note that this model describes each component of absorption and back- scattering as a linear sum of subcomponents, presumably with unique spectral dependencies [sym- bolized by the summation over N in Eqs. (4), (6), and (7)]. In this way, the absorption characteristics for different phytoplankton populations and the scatter- ing characteristics of multiple size distributions of suspended particles can be represented, or Eq. (6) can be re-expanded to Eq. (4).
Model configuration

Here explained the default configuration of GIOP.
Code
I think code is more visble for me
I skip the former part
1 | ''' |
Evaluating semi-analytical algorithms for estimating inherent optical properties in the South China Sea
这是一篇比较新也比较系统的评价文章,同时他们还做了match up和QA score
这是No-water absorption的结果
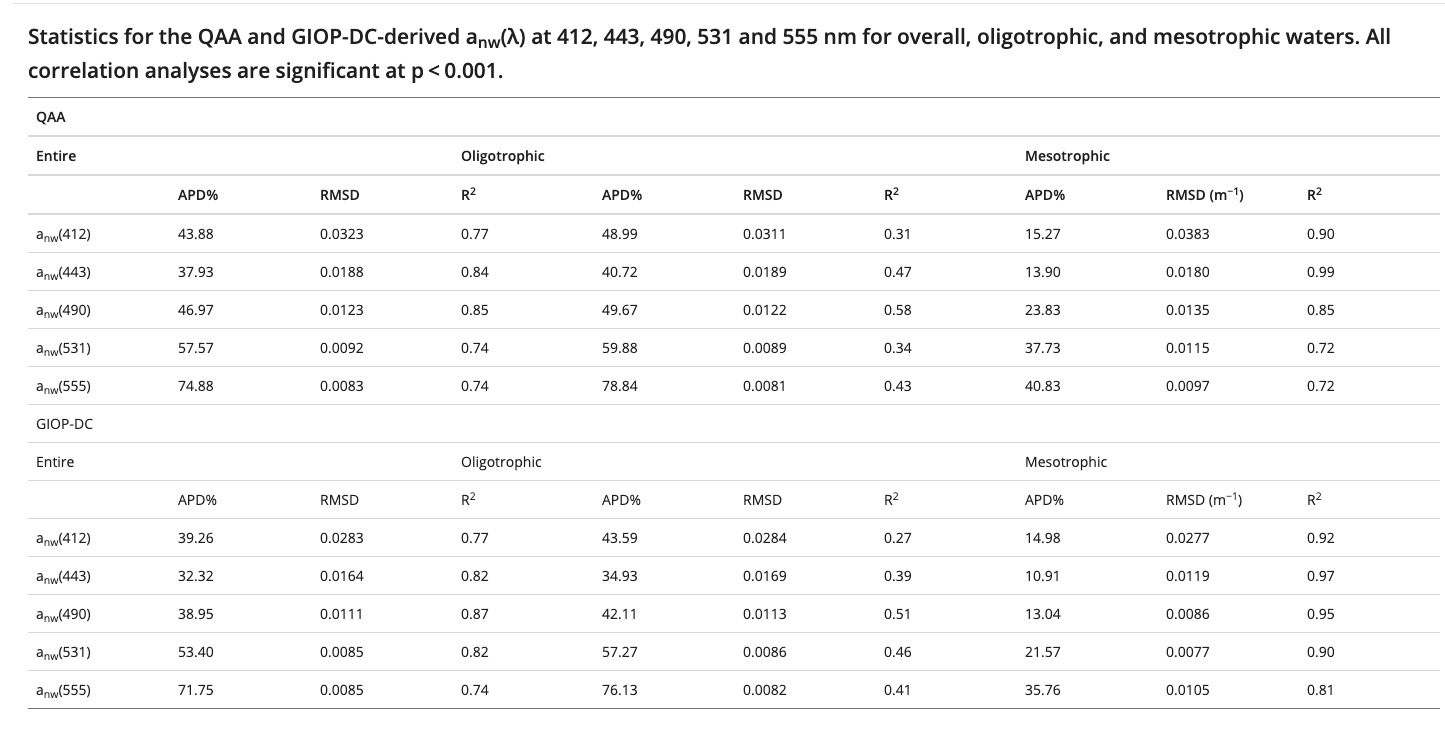
可看出来这俩几乎差不多
这是aph的结果
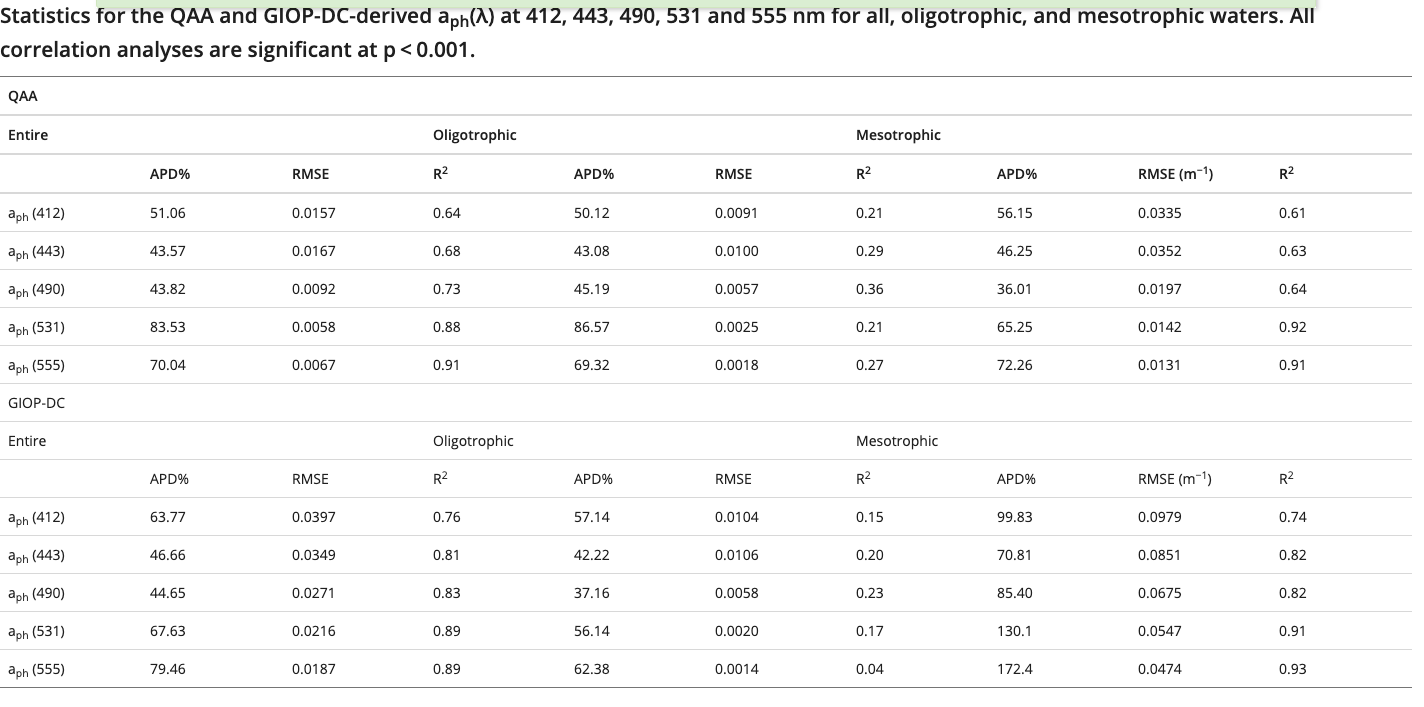
GIOP表现的会比 QAA在Mesotrophic好一些
bbp

反而是QAA
总而言之 他们发现没有特别大的区别
反而GIOP的Chla-aph关系式最好进行重新参数化