book-reading-note2
Chapter 7.1-7.2.4 of book 《Dynamics of Marine Ecosystems: Biological-Physical Interactions in the Oceans》
Tides, tidal mixing, and internal waves
Introduction
This chapter focus on the tides, tidal mixing and internal waves and today I will talk from the introduction to the physics of tidal currents.
Tides are created by the gravitational pull of the moon and the sun. The changing water level leads to interesting patterns of intertidal organisms( place a figure of intertidal zone ) but it is not the emphases of this chapter.
Besides the intertidal zone, the tides also generate currents in the water that interact with the bottom to produce turbulence. And if the currents are sufficiently strong, the turbulence could prevent any stratification , thus the wholes area may be permanently tidally mixed. There are some researches shows that a great number of stocks only live in such strong tidal mixing area. In this chapter we will explore the possible significance of this observation.
And if the tidal mixing is not so strong, the water column becomes stratified, the interaction of the tidal currents with the bottom topography could lead to the formation of internal waves. Internal waves could cause vertical mixing and redistribution of nutrients, which is important effects on phytoplankton production. Some times as the internal wave decays, they produce solitary waves and bores,which could have a strong influence of on the distribution of zooplankton and larval fishes.
Around the shallow bank, the interaction between tidal currents and bottom topography could generate unidirectional currents that form gyres. The combination of tidally mixed water over the top of a bank and a gyre around its periphery is thought to provide conditions particularly suitable for the eggs and larvae of fish. In this chapter we shall explore some of these interesting consequences of tidally induced water movement.
(Needs some more figures and references to tell the story)
The physics of tides
Tide-generating forces and the equilibrium tide.

First part is the physics of tides. Lets start from the most simple occasion. Here the earth and the moon are seen from above the north pole of the earth
- The water on the earth only receive the gravitational pull of the moon, remove the sun and the centripetal force from earth.
- The earth and moon are assumed to be stationary except for the earth’s rotation.
- The earth doesn’t have continents and is covered with a uniform layer of water.
- Without the Coriolis force and friction force.
Our observer is located in O. It is clear that the , the highest tide will always under the moon and the lowest tide will be on the opposite side to the moon as a result of gravitational pull of moon and centripetal force from earth. With the earth rotate, our observer will see one high tide and one low tide a day.
This elementary model could produce a tide but it is not a very good model because most places on the earth usually have two high and two low tides during the day.
One thing that need to consider is the rotation of the earth moon pair, about 29.5 day once. Because the earth’s mass is roughly 80 times that of the moon the common center of rotation is inside the earth about 1600 km below the surface along a line from the moon to the earth. The the common center of rotation is inside the earth about 1600 km below the surface along a line from the moon to the earth. And in order to make the earth and moon rotate around the center of mass, both of them will receive a centripetal force from the center of mass. This force is supplied by the gravity between earth and moon. But for us, the earth is stationary, that mean we choose our earth as reference system. So in order to make our earth stationary, we need add a fictitious force or inertial force. As a result, the water in our earth now receive two force, one is the gravity from moon, another is inertial force which backwards the center of mass.
Therefore, the shape of water on our earth likes a rugby.
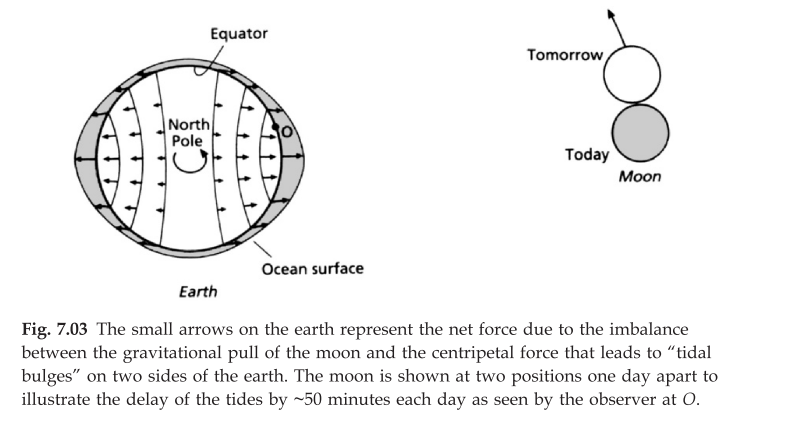
And this bulge is called tide bulge.
This model could help us describe two things. One is that we can observe two high tides and two low tides every day. Another is that why the tides do not occur at the same time every day. The earth and moon rotate around one another in a lunar month that is roughly 29.5 days. As our observer at O rotates through exactly one day back to O the moon has moved about 12° further around in its orbit to the position marked “tomorrow”.The high tide that is under the moon will still be under the moon tomorrow, but it will be observed later in the observer’s day.. Since the earth spins on its axis at about 4 minutes per degree the tides will appear about 50 minutes later each day.
The next refinement is. If we observe both from the side, not the pole, moon is not directly over the equator. The moon can be found at various angles to the north and south of the equator up to a maximum of 35° depending on the season and the time of the lunar month. So the tide bulge is no longer on the equator. No our observer in O could observe two high tide and two low tides every day. But the high tides are unequal height, as are the low tides. This difference is called the diurnal (daily) inequality.
This model only consider the effect of moon,without continents Coriolis force and friction force. Such tide is called equilibrium tide and this theory is called The Equilibrium Theory of Tides or “static” theory of tides.
It cannot predict It cannot predict the tide at any particular location but it does explain some of the main features of the tide such as
- diurnal variation
- diurnal inequality in the height
- daily delay
The next improvement of equilibrium theory of tide is considering the effects of the earth-sun system on top of the effects of the earth–moon system.
The mass of the sun is 27 × 106 times the mass of the moon but its distance from the earth is 400 times that of the moon. Because of this great distance, the gravitational attraction on a particle of water on the earth due to the sun is about one-half that due to the moon. So we can construct diagrams like those shown in Figs. 7.03 and 7.04 for the tide due to the sun, but the height of the tide will be only half that due to the moon. The important effect of the tide due to the sun arises because its tidal bulge moves relative to the moon’s tidal bulge through- out the lunar month.
When the two tidal bulges coincide they add together to create the extra high tides called the spring tides. When the tidal bulges are opposed their effects tend to cancel one another, creating the neap tides. Thus, the equilibrium tide model can also qualitatively explain the fortnightly inequality in addition to the other effects.
Tides in the real ocean
The next development of tide theory is dynamic theory of tide. It considered the continents, topography, Coriolis force and friction force, etc.
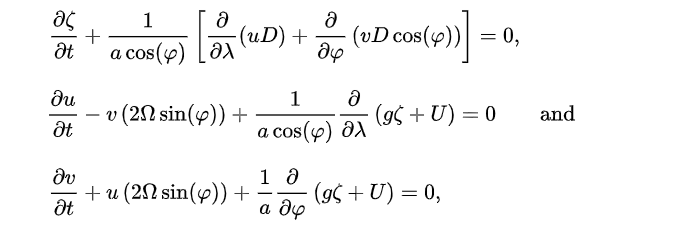
This is the Laplace’s tidal equations. But it is hard to solve. For prediction, one solution is that we can decompose the tide. We can think the real tide in our ocean is composed by a lot of tide constituents . Each tide constituents induced by each an imaginary planets. There are three main categories of constituents (Pond and Pickard 1983):
- semi-diurnal, period about 12 hours
- diurnal, period about 24 hours
- long period, greater than 24 hours.
The four most important constituents are:
- The lunar semi-diurnal ,M2, Period=12.42h
- The solar semi-diurnal, S2, Period=12.00h
- The lunisolar diurnal, K1, Period=23.93h
- The principal lunar diurnal, O1, period=25.82h
The M2 constituent is roughly twice the amplitude of the other three.
In different location around the word, the relative importance of constituents is quite different. So we have different patterns of tides. The four main classifications of the form of the tides are illustrated in the next figure.
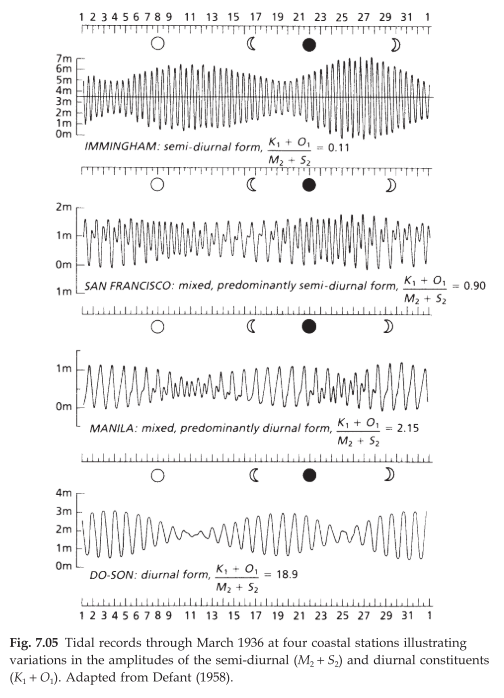
The first one has two high tides and two low tides every day and Both the highs are about the same height and both the lows are about the same height. Such a tide is called a semi-diurnal in form because there are two per day and both are about the same height.In this case the semi-diurnal constituents dominate the diurnal ones. This fact is often quantified with the ratio F = (K1+O1)/(M2 + S2 ), where each letter stands for the amplitude of the constituent. If F is small (0.11), as in the upper record, the sum of the amplitudes of the diurnal constituents (K1+O1 ) is small relative to the sum of the semi-diurnal ones (M2+S2 ).
The four records in Fig. 7.05 show a marked decrease from top to bottom in the amplitude of the semi-diurnal tidal oscillation relative to the diurnal oscillation, which is confirmed by the increase in F from 0.11 to ~19. At San Francisco there are always two tides per day but they are usually of unequal amplitude. At Manila there are two tides per day during the neap tides but only one rise and fall per day during spring tides. At Do-Son there is only one rise and fall of the tide per day throughout the month, which is a purely diurnal form of tidal oscillation. This occurrence is the rarest form of tide. The changing form of the tide between locations is due partly to the shape of the ocean basin in which the tidal wave is contained and partly to the latitude (Hendershott 1981).
Moving the tidal bulge over the earth: Kelvin waves
The former one is more focus on the coast, if we focus on a more large scale, the water depth is almost the same and the friction from the topography could be ignored. More idealized, if we assume the coast line is straight, we could get One solution of former dynamic tide equation set is that the velocity of tide is

here g is Gravitational acceleration and k is the depth of the water. and the Kelvin wave is a reasonable approximation for tidal waves in the vicinity of a straight coastline.
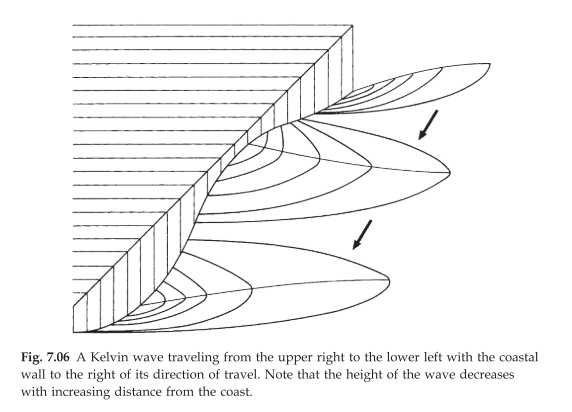
And here the Coriolis force is an important feature of the motion.
. The effect of the Coriolis force is to push the water to the right in the northern hemisphere
The Coriolis effect causes the amplitude of the wave to increase toward the shore and leads to the expression that the wave is “trapped” against the shore. Such a trapped Kelvin wave causes the water particles to move back and forth parallel to the coast as the wave goes by
The horizontal scale of the wave, or the approximate distance from the coast to where the sea level is undisturbed by the wave, is estimated by the Rossby radius.
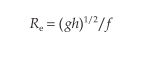
For the Kelvin wave in Fig. 7.06 we put g = 10 m s−2 , h = 4000 m, and f= 10−4 s−1 to get Re = 2000 km. This value is commonly called the external Rossby radius, or deformation scale